14-13. Решение транспортной задачи с помощью дискретного принципа максимума

Рассмотрим, как формализуется в терминах дискретного принципа максимума транспортная задача. Как было показано ранее, в транспортной задаче требуется определить оптимальные значения u^k_l(i=1, 2, ..., m; k=1, 2, ..., n), обращающие в минимум выражение

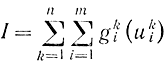
при условиях

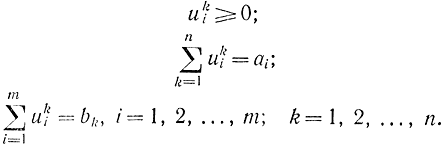
Здесь m - число складов (размерность задачи); пn- число пунктов назначения (пунктов потребления); a_i -запас товаров на i-м складе; b_k - потребность в товарах на k-м пункте потребления [Л. 88].

Введем динамический процесс распределения, переписав уравнения (14-30):

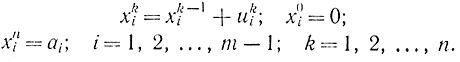
В этих уравнениях переменные состояния x_i представляют собой общее количество товаров, перевозимое с i-го склада на k-й пункт назначения. В них содержится m - 1 переменных u^k_i вместо m (числа складов), так как при заданных b_kодна из переменных u^k_i всегда может быть выражена через остальные с помощью соотношения

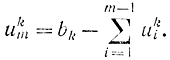
Вводим m-ю переменную состояния

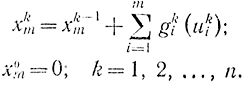
Общая стоимость перевозок

В данной задаче требуется определить значения u^k_i(i=1, 2,... m-1; k=1, 2,..,n), обращающие в минимум xⁿ_m. Функцию Понтрягина запишем в виде

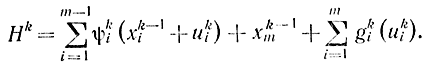
После этого уравнения (14-38) перепишутся:

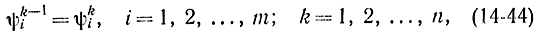
а условия (14-40) примут вид:

Из полученных соотношений (14-44) и (14-45) имеем:

Величины xⁿ_i заданы, и требуется так подобрать значения ψⁿ_i или uⁿ_i, чтобы в конце вычислений xⁿ_i(i = 1, 2,..., m-1) равнялись заданным.

Пример 14-4. Допустим имеется два склада m=2 и восемь пунктов потребления n=8. Функции себестоимости g^k_i(u^k_i) задаются формулой (14-13) и табл. 14-8. Так же как и в примере 14-2, зададимся запасами на складах а₁=40, а₂=50. Очевидно, что достаточно определить оптимальное распределение грузов, доставляющее минимум той части функции Понтрягина, которая зависит от управления:

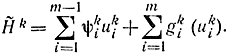
Для нашего случая

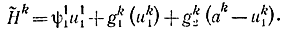
Оптимальное управление должно доставлять минимум этой функции для каждого k=1, 2, ..., 8 при фиксированном ψ¹₁. Заметим, что в соответствии с формулой (14-44)

Неопределенная до начала вычислений величина ψ₁ подбирается таким образом, чтобы в конце вычислений удовлетворялось равенство

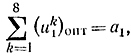
при этом

Величина ψ₁ определяется методом пристрелки. Заметим, что для заданного вида функций g^k_i(u^k_i) можно заранее определить интервал неопределенности, в пределах которого выполняется условие

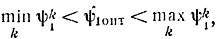
причем

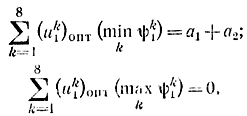
Выбирая каждый раз ψ^k₁ в середине интервала неопределенности и анализируя величину Δ=Σu^k₁(ψ₁)-a₁, можно сократить интервал неопределенности вдвое. При некоторых условиях этот процесс сводится к ψ_1опт. Такой процесс пристрелки содержит в себе трудности, связанные с краевыми условиями, в чем заключается один из основных недостатков принципа максимума.

Задача решается с погрешностью δ=0,2, т. е. считается, что оптимальное решение найдено, если |Δ|≤δ. Результаты решения приведены в табл. 14-11.

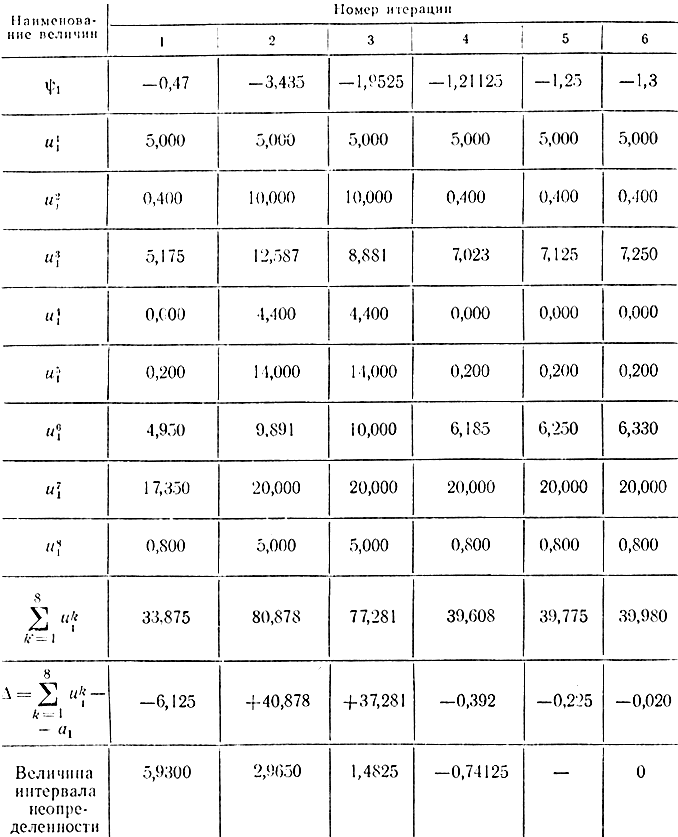
Таблица 14-11

Распределение поставок приведено в табл. 14-12.

Общая себестоимость всех перевозок С=274, 6864. Расчеты произведены на машине М-20, Как и следовало ожидать, данные табл. 14-12 совпадают с данными табл. 14-8 примера 14-2, в котором использовалось дискретное динамическое программирование.

Таблица 14-12

На сегодняшний день не закончилась еще дискуссия о преимуществах и недостатках каждого из двух методов: принципа максимума и динамического программирования. В одних задачах удобней применять один метод, в других - другой. Аналитически они достаточно близки друг к другу и могут получаться один из другого путем простых выкладок. Но все же можно утверждать, что принцип максимума математически более строго обоснован, он исходит из классического вариационного исчисления и использует только особый вид вариации. Динамическое программирование основано на постулате, т. е. эвристическом утверждении, которое обычно формулируется как принцип относительности Беллмана.

Основное различие между этими методами лежит в вычислительной процедуре. И с этой точки зрения в большинстве случаев предпочтение следует отдать принципу максимума. Дело в том, что, пользуясь динамическим программированием, необходимо на каждом шаге вычислять значения функций для всех значений переменных состояния. Принцип же максимума позволяет все время иметь дело с одним и тем же решением на всех ступенях, просто улучшая его на каждой ступени. Благодаря введению переменных ψ^k_i объем требуемой для вычислений памяти вычислительной машины для принципа максимума растет линейно с увеличением размерности задачи, а для динамического программирования - экспоненциально. Поэтому время счета в первом случае, как правило, меньше. Однако для решения задач с ограничениями на переменные состояния принцип максимума встречается с трудностями, которые совершенно отсутствуют в динамическом программировании.