Глава пятнадцатая. Прямые методы отыскания экстремума функции

Рассматривать методы нахождения экстремума функции, а не функционала мы начали, по существу, уже в разделе дискретных методов оптимизации, отыскивая оптимальное решение с помощью динамического программирования и принципа максимума. Прямые методы

применяются на каждом этапе отыскания оптимальных значений и, в частности, при решении функционального уравнения Веллмана. Известно достаточно много прямых методов. Здесь будут рассмотрены основные.

Рассмотренные ранее непрямые методы решали задачу в соответствии с определенным дифференциальным или рекуррентным соотношением, которому удовлетворяло оптимальное решение, т. е. имели аналитический характер. В прямых методах, как правило, отсутствуют такие аналитические соотношения. Прямые вариационные методы, так же как и процедуры решения задач с помощью дискретных динамического программирования и принципа максимума, по существу близки к прямым методам отыскания экстремума и отличаются от них только своей ориентацией на определенные аналитические уравнения. Кроме того, особенностью прямых методов, рассматриваемых в данной главе, является отсутствие ограничений на изменение переменных, характерных для линейного и нелинейного программирования. Ограничения здесь имеют простейший вид: a_j≤x_j≤b_j.

Прежде чем перейти к методам, обратим внимание на близость задач отыскания экстремума и нуля функции. Допустим, имеется m совместных уравнений:

требуется найти x_j(i=1, 2,..., n), удовлетворяющие им. Очевидно, что значения x_j будут нулями функций φ_i. Задачу можно свести к нахождению экстремума функции Φ, представляющей собой сумму квадратов функций φ_i. Так как φ_i могут быть комплексными .функциями, то

где φ^*_i - функции, комплексно-сопряженные φ_i. И наоборот, если требуется определить экстремум дифференцируемой функции Φ (x₁, x₂,...,x_n), эту задачу в простейшем случае можно свести к определению корней уравнений

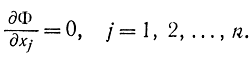
Однако особый интерес представляют методы поиска при отсутствии производных от функции цели Ф [Л. 80, 92].

Поиск экстремума может быть детерминированным (при отсутствии шумов) и стохастическим (при наличии ошибки замеров значений функции). Различают пассивный или параллельный поиск, когда стратегия известна до получения результатов эксперимента, и активный или последовательный поиск, когда будущие стратегии уточняются в зависимости от результатов предыдущих экспериментов.

Вначале ограничимся одномерным детерминированным унимодальным случаем (когда на заданном интервале или множестве имеется

одно экстремальное значение). Будем называть функцию одной переменной f(х) на интервале [0, 1] строго унимодальной, если она строго возрастает (или убывает) при x≤x⁰ и x≥x⁰, где x⁰ точка экстремума из интервала [0, 1], т. е. 0≤x⁰≤1- Очевидно, что всякая выпуклая функция на интервале изменения [0, 1] одновременно и унимодальна. Однако обратное утверждение может быть и несправедливо.

Если допустить разрывы непрерывности функции f(x) и ее производной, то могут встретиться унимодальные на интервале [0, 1] функции, не обладающие свойством выпуклости (рис. 15-1). Унимодальность обеспечивает выполнение следующего очень важного условия: если оба отсчета функции y=f(x)

взяты по одну сторону от максимума, то большему значению y соответствует более близкое к оптимуму значение x. Эта зависимость, которая легко доказывается от противного, позволяет сформулировать критерий эффективности методов поиска и иллюстрируется рис. 15-2, из которого видно, что с учетом условия унимо-дальности после двух экспериментов исключаются отрезки: [x², 1] (рис. 15-2, а), [0, x¹] (рис. 15-2, б) и [x², 1] (рис. 15-2, в).

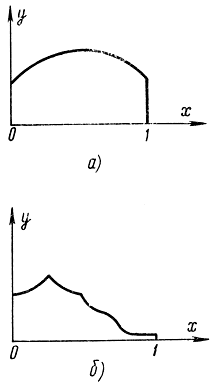
15-1. Графики выпуклой (а) и невыпуклой (б) унимодальной функции

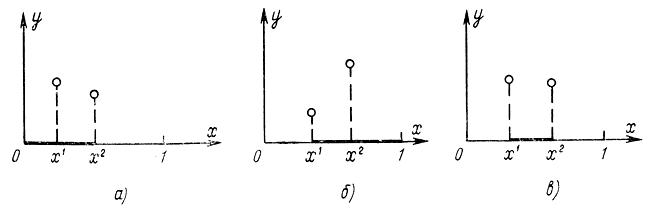
Рис. 15-2. Возможные варианты уменьшения интервала неопределенности при двух экспериментах

По существу мы здесь вторгаемся в область кибернетики, называемую планированием эксперимента, которую, как правило, рассматривают в математической статистике.