г) Поиск по дискретным точкам

Все ранее рассмотренные методы исходили из того, что величина x^k может принимать любое значение внутри интервала [0, 1] и интервал неопределенности может изменяться непрерывно. Однако чаще требуется осуществлять выбор на конечном дискретном наборе значений x^k. Например, требуется поделить число квартир или составить сборную страны по футболу из игроков команд первой группы, - число комбинаций здесь всегда конечное. Иногда непрерывный поиск искусственно превращают в поиск по дискретным точкам, так как последний выделяет одну точку экстремума, а не интервал неопределенности, который неудобен для решения задач, имеющих дело с конкретными понятиями.

Допустим, задано s дискретных точек: x₁, x₂,...,x_n значения которых необязательно должны быть целыми числами. Например, среднее число ящиков, которое загружается в единицу времени, может принимать значения: 3,0; 3,4; 3,6; 4,2; 4,4; 4,6; 5,0. Сопоставим каждому дискретному значению целые числа (табл. 15-2):

Таблица 15-2

В интервале от нуля до единицы расположим равномерно k точек (рис. 15-12). Для нашего примера число k + 1 равно числу Фибоначчи F₅=8, исходный интервал неопределенности отличается от единицы и равен L¹=F_N(N—5). Поэтому два первых эксперимента отстоят от концов исходного интервала неопределенности на величины F_NL²_опт где

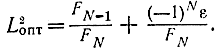
Полагая ε=0, получаем:

В силу этого соотношения первые два эксперимента совпадут с дискретными точками. В данном примере F_N=F₄= 5 и точками первых двух экспериментов будут точки 3 и 5, отстоящие от концов интервала на величину F4 = 5. Точно так же третий эксперимент попадает в дискретную точку 6, четвертый — в точку 7, пятый и последний — в точку 6. Процесс закончится, когда длина интервала неопределенности станет равной единице. Отсюда в соответствии с формулой (15-8) при ε=0 имеем:

Следует специально остановиться на условии ε=0, благодаря которому последний эксперимент попадает в точку, где уже производился один из предыдущих экспериментов. Это позволяет не производить последнего эксперимента. Действительно, интервал неопределенности F_NL^N-1_опт остающийся после N-1 шагов, в соответствии с формулой (15-15) равен двум. Причем, как видно из рис. 15-12, концы этого интервала уже испытаны и отвергнуты, поэтому оптимумом Должна быть середина-интервала.

Напомним, что в методе Фибоначчи 8 появилось для выполнения последней пары экспериментов: (N—1)-го и N-го, которые пришлось расположить в силу непрерывности х на расстоянии ε/2 от середины интервала L^N-1_опт. Именно поэтому и из требования различения двух последних экспериментов по х возникла необходимость введения ε.

Если обозначить через s_N-1 максимальное число точек, которые после N - 1 экспериментов можно свести к единственному экстремуму, то очевидно, что s_N-1=F_N-1, так как в интервале длиной F_N, содержащем F_N-1 точек, можно по методу Фибоначчи найти оптимальную точку после N - 1 экспериментов. Иначе эту формулу можно переписать как s_N-F_N+1-1. Сравнительные значения этой величины приведены в табл. 15-1.