15-4. Метод рандомизации

В предыдущем разделе мы убедились, что метод Фибоначчи с успехом может применяться при поиске на дискретном множестве точек. Однако если число исходных точек сильно отличается от ближайшего, строго большего числа Фибоначчи, то приходится добавлять фиктивные точки и тем самым увеличивать количество экспериментов. Так, при 8 опытах добавляется еще,5, т. е. общее число точек доводится до ближайшего, строго большего числа Фибоначчи, 13. Но можно ввести элемент случайности и выбирать экспериментальные точки в соответствии с определенным законом распределения (например, с помощью бросания монеты или кости). При этом в среднем можно получить выигрыш в числе точек эксперимента по сравнению с детерминированным поиском по методу Фибоначчи. В этом и заключается метод рандомизации. Процедура поиска экстремума основывается на определенной вероятностной модели расположения экстремума. Считается, что природа, как партнер в игре, предлагает для поиска определенный вероятностный закон распределения экстремума. Такая трактовка процедуры поиска вполне оправдана, так как неизвестно, где находится экстремум. Стратегия строится вероятностным образом, так как экстремум с определенной вероятностью может появиться в любом месте. Такой подход по существу совпадает с игровым методом и процедурами проверки статистических гипотез.

Для простоты рассмотрим случай унимодальной функции [Л. 92], заданной на трех дискретах: 1, 2, 3. Все варианты проведения эксперимента можно разбить на три: (1, 2), (1, 3) и (2, 3). Если экстремум окажется в точке 1, то при выборе стратегии (1, 2) (т. е. первые два эксперимента производятся в точках 1 и 2), третьего эксперимента можно не делать. Двух экспериментов окажется достаточно, если экстремум находится в точке 3 и было принято решение провести эксперименты в точках (2, 3). Во всех остальных случаях требуется провести три эксперимента. Окончательные данные о числе необходимых опытов по всем вариантам сведены в табл. 15-3.

Таблица 15-3

Таблица 15-3 — это по существу настоящая игровая матрица. Платежом в такой игре является число необходимых экспериментов N. Матрица получилась не вполне удачной, так как в ней отсутствует седловая точка, поэтому для решения данной игровой,задачи необходимы специальные приемы. Можно сразу исключить стратегию, состоящую в выборе второй пары точек (1, 3), так как в этом случае при любом положении экстремума заведомо получаются три эксперимента.

Для упрощения задачи вначале предположим, что во второй точке максимума быть не может. Остается установить вероятности выбора стратегий (1, 2) и (2, 3). Так как нет никаких оснований для предпочтения одной стратегии перед другой, положим вероятность выбора каждой из них, равную половине. Докажем это положение следующим образом. Будем считать, что из общего числа опытов n экстремум в точке 1 встречается n₁ раз. С помощью датчика случайных чисел выберем стратегию (1,2) n₁p раз и ограничимся двумя опытами. В остальных n₁(1—р) случаях выберем стратегию (2, 3) и ограничимся тремя опытами. Величину р найдем исходя из минимаксного критерия. Основываясь на приведенных рассуждениях, считаем, что требуется произвести 2n₁р+3n₁(1—р) опытов. Разделив эту величину на n₁ получим среднее число опытов e₁, которые необходимо проделать при условии, что экстремум действительно находится в точке 1:

Аналогично, если обозначим через n₃ число случаев нахождения оптимума в точке 3, то для необходимого количества опытов получим выражение 3n₃p+4-2n₃(1—p), а для среднего числа опытов формулу

Для удовлетворения минимаксного критерия требуется найти такое значение р=р_опт, при котором минимизируется функция

Нетрудно убедиться, что минимальное значение, равное 2,5, для этого выражения достигается при р_опт=0,5.

Теперь учтем возможность нахождения экстремума в точке 2. Для этого введем в рассмотрение относительную частоту f_i, с которой экстремум появляется в точке i,

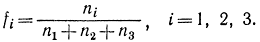
Среднее число экспериментов при минимаксной рандомизированной стратегии определится как

Интересно заметить, что эта величина не зависит явно от f₁ и f₃, т. е. если природа или противник выбирает наихудшую для нас стратегию (частоты f₁ и f₃), среднее число опытов остается неизменным при неизменности f₃.

Теперь отойдем от рандомизированной стратегии и будем считать, что относительные частоты f_i известны заранее. Тогда, учитывая, что

для среднего числа экспериментов напишем:

Отсюда, если f₁>f₃, минимум e достигается при р=1; если f₁=f₃, значение p не оказывает влияния на e; если f₁<f₃, минимум е достигается при p=0. Поэтому оптимум будет иметь место для

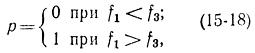
чему соответствует

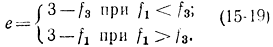
Если подставить выражение (15-17) в (15-16), то

С помощью формул (15-19) и (15-20) можно получить выражение для выигрыша при детерминированном поиске, когда по сравнению с рандомизированным поиском заранее известны частоты f_i:

Из формулы (15-18) видно, что при известных f₁ и f₃ стратегия становится детерминированной (чистой). Если эти частоты неизвестны заранее, то применяется смешанная стратегия.