15-5. Особенности многомерного поиска

Рассмотрим методы отыскания экстремума в случае, когда функция- критерий зависит от нескольких переменных y=y(x₁, x₂,..., x_n). Для двух переменных (число опытов n=2) функция y=y(x₁,x₂) геометрически изображается поверхностью в трехмерном пространстве.

В общем случае имеет место гиперповерхность в (n+1)-м гиперпространстве.

Поиск экстремума в многомерном случае сложнее, чем в одномерном, по следующим причинам [Л. 92]. Предположение унимодальности критерия в заданной области изменения переменных является менее вероятным и достоверным при большом количестве переменных. Эффективность в многомерном случае также можно оценивать по величине остающейся площади поверхности неопределенности. Однако так как поверхности критерия или отклика заранее неизвестна, нельзя до опытов предсказать форму и величину поверхности неопределенности, которые определяются после n опытов. Поэтому не существует объективного метода оценки эффективности многомерного поиска и оптимальной в определенном смысле стратегии поиска.

Последнее обстоятельство, усложняющее многомерный поиск, связано с уже известным нам проклятием размерности. В данном случае геометрически его можно проиллюстрировать с помощью рис. 15-13. Представим себе единичный исходный отрезок неопределенности по одной координате х. Возьмем от него часть длиной 0,1, т. е. 10% первоначальной длины. Однако если рассматривать двумерную исходную область поиска в виде квадрата со сторонами, равными единице, то квадрат со сторонами 0,1 составит только 1 % общей площади. Это свидетельствует о том, что для просмотра всей площади (путем просмотра сторон квадрата) требуется, грубо говоря, в 10 раз больше шагов, чем в одномерном случае. Если перейти к трехмерному пространству, то отрезки длиной 0,1 первоначальной длины куба составят куб объемом 0,001 исходного, т. е. 0,1%, и т. д.

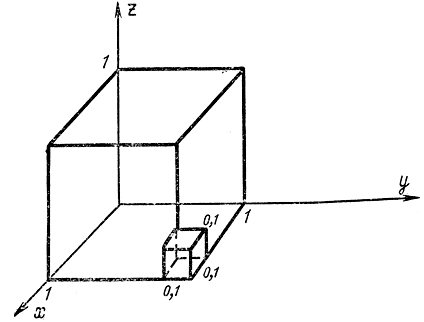
Рис. 15-13. Пояснение к проблеме размерности при многомерном поиске