15-6. Случайный поиск

Достаточно распространен на практике многомерный случайный поиск. Допустим, ведется поиск в трехмерном пространстве - единичном кубе, разделенном на 1 000 одинаковых кубических областей. Каждой области можно поставить в соответствие значение критерия эффективности. Вероятность найти одну из ста лучших ячеек

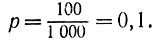
Вероятность противоположного события представится как

Если имеются две пробы, то вероятности неудачных событий (не нашли ячейку) при двух попытках можно считать независимыми и вероятность неудачи будет равна (0,9)² = 0,81, а вероятность удачи - 1-0,81 = 0,19. Заметим, что исходный интервал неопределенности здесь сводится к 10%-ному. В общем случае вероятность получения 10%-ного интервала неопределенности

После n = 16 опытов p(0,10)=0,84; после n = 44 опытов p(0,10)=0,99, т. е. получаем практически достоверное событие.

В одномерном пространстве уменьшение исходного интервала в 10 раз требовало бы 18 опытов при параллельном (пассивном) поиске и шести при последовательном. Из этого примера видно, во что обходится увеличение размерности. В общем случае, если требуется сократить исходную область неопределенности в 1/f раз, необходимо иметь

т. е.

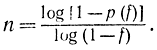
Метод случайного поиска обладает тем преимуществом, что не требует никаких предположений о поверхности отклика. В частности, эта поверхность может быть много экстремальной. С помощью этого метода, выбирая достаточно малые ячейки, можно обнаружить все локальные экстремумы и выбрать из них наилучший. Однако в данном изложении он по существу является пассивным методом со всеми его недостатками. Усовершенствовать его можно, преобразовав в последовательный, для чего каждую последующую точку следует выбирать вблизи предыдущей случайным, но оптимальным образом и превращать в новый центр рассеивания и т. д. Причем для выбора последующей точки необходимо использовать методы планирования эксперимента.