15-7. Метод исключения касательными

Большинство методов многомерного поиска использует геометрическую интерпретацию, в частности изображение поверхности отклика y=y(x₁, x₂, ..., x_n) с помощью линий уровня y=const (рис. 15-14). В случае двух переменных x₁, x₂ уравнение касательной плоскости к поверхности отклика имеет вид:

Обычно задают отклонения новой точки х¹ с координатами (x¹₁, x¹₂) относительно начальной точки x⁰ с координатами (x⁰₁, x⁰₂):

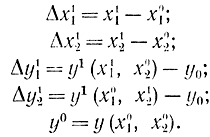
Тогда приближенное уравнение касательной плоскости в точке x⁰ в приращениях имеет вид:

причем коэффициенты m₁ и m₂ определяются следующим образом:

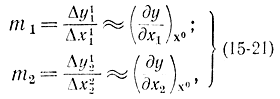
т. е. они примерно равны соответствующим частным производным от функции отклика.

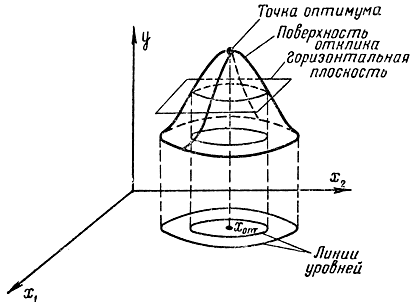
Рис. 15-14. Линии уравнений для двумерного случая

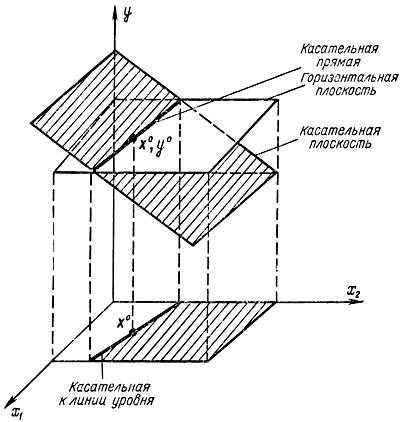
Рис. 15-15. Горизонтальная и касательная плоскости к поверхности отклика и проекция их линии пересечения

Метод исключения касательными к линиям уровня состоит в том, что исключается поверхность от-клика, лежащая, по одну сторону от вертикальной плоскости, проведенной через касательную к линии уровня в точке x⁰, y⁰. Нетрудно убедиться с помощью рис. 15-15, что касательная к линии уровня в точке x⁰ является проекцией на плоскость x₁, x₂ линии пересечения горизонтальной и касательной плоскостей к поверхности отклика, проходящих через точку y⁰.

После трех экспериментов (x⁰₁, x⁰₂), (x⁰₁, x¹₂), (x¹₁, x⁰₂), с помощью которых по формулам (15-21) определены m₁ и m₂, интерес представляют только те Δx₁ и Δx₂, для которых Δy>0 или m₁Δx₁+m₂Δx₂40. Границей исключаемой и оставляемой областей будет прямая m₁Δx₁+m₂Δx₂=0. Нетрудно убедиться, что она совпадает с касательной к линии уровня y=cons =y₀ в точке x⁰ (рис. 15-16).

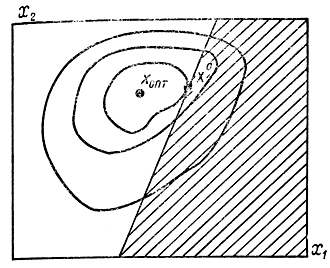
Рис. 15-16. Пояснение к методу исключения касательными

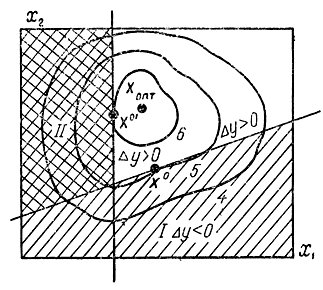
Рис. 15-17. Метод исключения касательными

Чтобы завершить процедуру поиска, необходимо выбрать способ нахождения следующей точки для испытания в оставленной области Δy>0 (рис. 15-17, области I и II).

Существует несколько способов выбора начальной точки для эксперимента.

В простейшем случае выбирается средняя точка области с координатами (x⁰₁, x⁰₂,...,x⁰_n), где

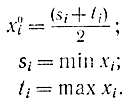
У метода исключения касательными есть один существенный недостаток, заключающийся в том, что он применим только к строго унимодальным функциям отклика. Строго унимодальная функция обладает таким свойством, что по прямой, проведенной из любой точки а в области эксперимента к вершине х_опт, траектория будет возрастающей. Применение рассмотренного метода к нестрого унимодальным функциям может привести к исключению из рассмотрения экстремальной точки х_опт (рис. 15-18). Иногда говорят о наличии оврагов у функции отклика в этом случае. Однако в отличие от наиболее распространенного метода градиента эта процедура менее чувствительна к изменению масштаба.

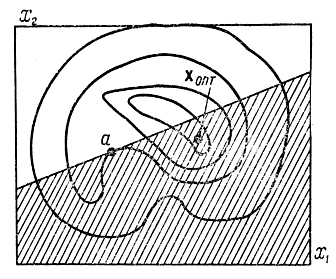
Рис. 15-18. Неприменимость метода исключения касательными при наличии овратов