15-8. Градиентный метод

Метод градиента предполагает движение по нормали к линиям уровней (рис. 15-19). Основная проблема заключается в выборе величины каждого дискретного шага. Шаги могут быть постоянными и переменными. Этот метод вполне естествен. Здесь характерен пример с восхождением на гору: метод градиента обеспечивает наибыстрейшее достижение вершины. В этом случае линиями уровней будут проекции линий пересечения горизонтальной плоскости с поверхностью горы.

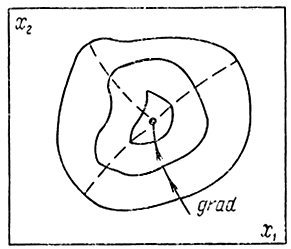
Рис. 15-19. Метод градиента

Аналитически метод градиента может быть записан в виде

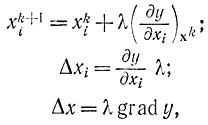
где k - некоторый постоянный или переменный параметр, определяющий величину шага; k - номер шага; y - функция цели.

Если аналитически производные определить невозможно, в простейшем случае их вычисляют приближенно:

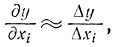
где Δy - приращение функции y при изменении переменной x_i на величину Δx_i. В точке экстремума градиент равен нулю.

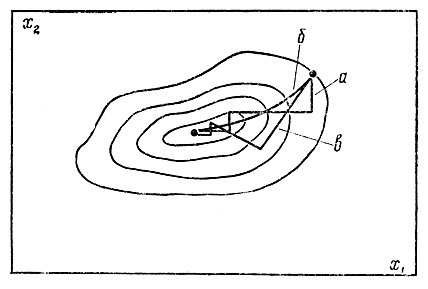
Рис. 15-20. Методы покоординатного (а), градиентного (б) и наискорейшего спусков (в)

Модификаций метода градиента много, но нет единообразия в терминологии. Здесь будут рассмотрены различные модификации, которые не всегда относят к классу градиентных методов и которым в литературе можно найти иное название.

Если подъем или спуск происходит поочередно по каждой координате x₁, x₂,..., x_n, то имеет место метод, часто называемый по координатным спуском (подъемом) или методом Гаусса - Зейделя (рис. 15-20, ломаная линия а). Движение осуществляется по одной координате x_v

до тех пор, пока не станет равной нулю соответствующая производная, т. е.

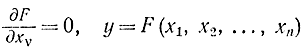
(все остальные координаты сохраняют постоянное значение x_j=const). После этого спуск начинается по другой координате. Обычно начинают с x₁ потом x₂ и т. д. После того как произведен спуск по всем координатам, начинают повторно с x₁ и т. д. Процесс поиска заканчивается, когда все производные будут равны нулю, т. е.

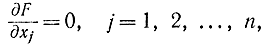
точнее, все производные будут меньше порога чувствительности.

Следующая модификация - метод наискорейшего спуска. Направление градиента определяют в начальной точке [grad F]_x⁰ и далее в этом направлении осуществляют спуск до тех пор, пока производная dF/dx, взятая вдоль этого направления, не обратится в нуль (линия в). После этого снова определяют направление градиента и осуществляют по нему спуск до нулевого значения производной и т. д.

Классический метод градиента предполагает движение по кривой градиента, нормальной к линиям уровней (линия б на рис. 15.-20), и при малом шаге Δx_j=x^k+1_j-x^k_j может быть описан следующим дифференциальным уравнением:

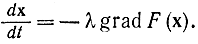
Это уравнение используют при реализации градиентного метода на непрерывных устройствах.