а) Метод Ньютона

Близким к методу градиента является метод Ньютона, который широко используется для отыскания нулей функции. Для простоты рассмотрим функцию одной переменной F(х) (рис. 15-21). Итерационный процесс отыскания нуля функции [Л. 93] определяется формулой

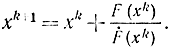
Геометрически процесс отыскания нуля функции по методу Ньютона заключается в проведении касательной к кривой y=F(х) в точке x^k уравнение которой задается соотношением

Точку пересечения касательной с осью абсцисс принимают за новую точку, в которой проводят следующую касательную и т. д.

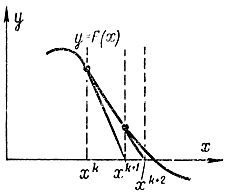
Рис. 15-21. Метод Ньютона

Этот метод в отличие от метода градиента не гарантирует сходимости. Для улучшения сходимости используют модифицированный метод

Ньютона, который вводит шаг 0<λ^k<1. При этом процесс отыскания нуля задается формулой

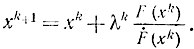
Существуют методы выбора при которых обеспечивается сходимость.