б) Метод секущих
Более простым для вычислений по сравнению с методом Ньютона является метод секущих, хотя он обладает более медленной сходимостью.
Через x0 и x1 обозначим две точки, в которых функция одной переменной y=F(х) имеет разные знаки (рис. 15-22). Уравнение секущей, проведенной через две точки [x0, F(х0) ], [х1, F(х1)], будет иметь вид:
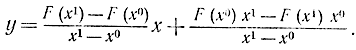
Точку х2 пересечения этой прямой с осью абсцисс определим из формулы
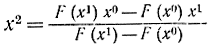
и примем за следующее приближение. Очередную секущую проведем через точки [х0, F(х0)] и [х2, F(х2)] и т. д. В общем случае итерационный процесс задается формулой
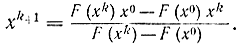
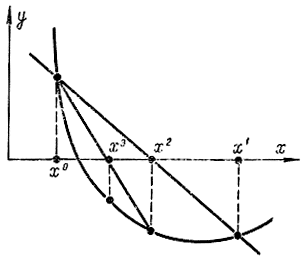
Рис. 15-22. Метод секущих
В отличие от метода Ньютона здесь не требуется на каждом шаге вычислять производные, достаточно определить только значение самой функции.
Можно показать, что метод Ньютона является методом градиентного спуска по поверхности параболоида Φ=Σ[ξi]2 в пространстве переменных ξi где
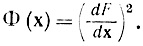
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'