в) Теорема двойственности

Докажем теорему двойственности для случая неотрицательных переменных прямой и двойственной задач, т. е. положим в соотношениях (16-21) - (16-24) l = k = 0. В этом случае имеем:

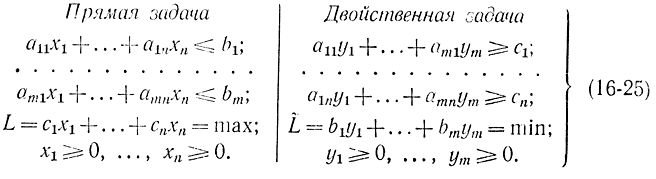
После введения дополнительных переменных x_n+v (v = 1, 2, ..., m) прямой и y_m+μ(μ = 1,2,..., n) двойственной задач в соответствии с формулой (16-19) обе задачи могут быть записаны в следующем виде:

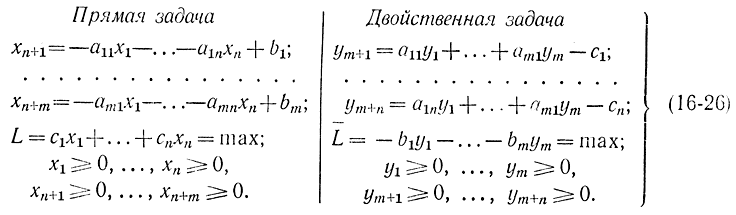
При этом в двойственной задаче также ищется минимум линейной формы, в которой в отличие от задачи (16-12) изменены знаки при коэффициентах линейной формы, что справедливо в силу соотношения

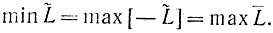
Требуется доказать, что

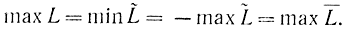
Вводя дополнительные переменные t и s, которые принимают значения, равные единице, перепишем соотношение (16-13) в следующем виде:

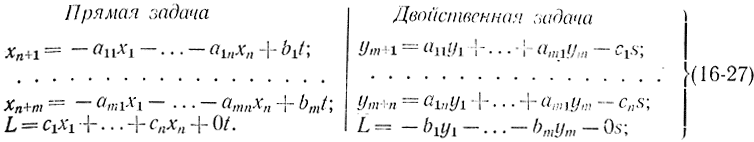
Две системы соотношений (16-27) являются взаимно двойственными в том же смысле, что и в предыдущем разделе. Между неизвестными x₁, ...,x_n+m, t, L прямой и y₁, ...,y_n+m s, L двойственной систем существует следующее соответствие:

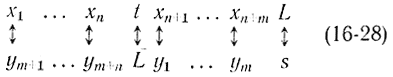
Эта жесткая связь определяется зависимостью между коэффициентами прямой и двойственной систем, которая имеет вид:

При оптимизации в прямой задаче требуется среди всех решений прямой системы (16-27), удовлетворяющих условиям x₁,...,x_n+m≥0, t = 1 найти такое, для которого L принимает максимальное значение. Соответственно при оптимизации в двойственной задаче требуется среди всех решений двойственной системы (16-27), удовлетворяющих условиям y₁,...,y_n+m≥0, s = 1, найти такое, для которого L принимает максимальное значение.

Решение прямой задачи оптимизации можно определить с помощью симплекс-метода. Его можно получить такой заменой базиса, при которой все свободные члены в соотношениях прямой системы (16-26) станут неотрицательными, так как только при неотрицательных свободных членах для нулевых значений не базисных переменных, стоящих в правых частях, базисные переменные, стоящие в левых частях, будут неотрицательны. Кроме того, экстремальное значение функции цели достигается при такой замене базисных переменных, при которой все коэффициенты при не базисных переменных в выражении для L отрицательны.

Применительно к прямой системе (16-27) процедура поиска оптимального решения означает такую замену базиса (переменных x₁,...,x_n+m), при которой все коэффициенты при t (кроме, может быть, последнего) становятся неотрицательными, а все коэффициенты в выражении Для L (кроме, может быть, последнего) не положительными. Обозначим такую систему соотношений через А. Искомый экстремум линейной формы L в ней будет равен значению коэффициента при t в выражении для L. Если соответственно заменить базис в двойственной системе (16-27), то получится система В, двойственная А в силу доказанного в предыдущем разделе положения. В системе В все коэффициенты при s (кроме, может быть, последнего) будут неотрицательны, а все коэффициенты при не базисных переменных в выражении для L (кроме, может быть, коэффициента при s) будут не положительны. Но это означает, что базисное решение системы В будет оптимальным для двойственной задачи (16-26) и коэффициент при s в выражении для L равен максимуму L. Если учесть взаимную двойственность систем А и В и связь переменных (16-28), то можно утверждать, что коэффициент при s в выражении для L (в системе В) лишь знаком отличается от коэффициента при t в выражении для L (в системе А), т. е. -max L = max L^-, что и требовалось доказать.