г) Двойственный симплекс-метод

Теперь мы подготовлены к изложению двойственного симплекс-метода или, как его называют, метода последовательного улучшения оценок. Смысл его заключается в том, что вместо прямой задачи решают двойственную и затем в соответствии с соотношениями (16-28) по оптимальным значениям переменных двойственной задачи определяют оптимальные значения прямой задачи, причем оптимальное базисное решение одной задачи получается приравниванием ее новых базисных переменных коэффициентам при соответствующих не базисных переменных в линейной форме двойственной задачи, взятым со знаком "-".

Двойственный симплекс-метод целесообразно' применять, когда в исходной задаче число ограничений значительно больше числа неизвестных. Очевидно если в этом случае перейти к двойственной задаче, то симплекс-процедура будет проще, чем для прямой задачи. Кроме того, двойственный симплекс-метод широко применяется в различных методах решения задач целочисленного программирования.

Часто решение двойственной задачи называют псевдопланом, чтобы отличать его от решения прямой задачи, называемого просто планом.

Проще всего проиллюстрировать двойственный метод на примере.

Пример 16-3. Рассмотрим следующую задачу линейного программирования:

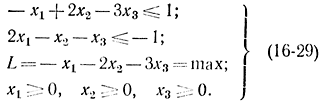
Составим задачу, двойственную (16-29):

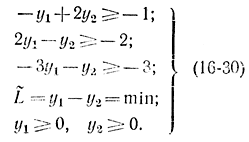
Вводя добавочные переменные y₃, y₄, y₅ сведем ограничения в виде неравенств к ограничениям в виде равенств. Тогда задача (16-30) примет вид:

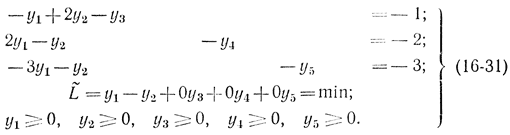
Решая задачу (16-31) симплекс-методом, получим симплекс-таблицу (табл. 16-4).

Таблица 16-4

Из последней строки табл. 16-4 получим выражение линейной формы через не базисные переменные

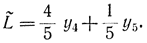
Отсюда, если учесть соответствие между переменными

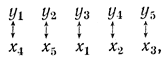
получим решение исходной задачи в виде

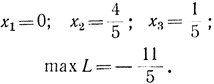
В этом примере использован по сравнению с примером 16-2 другой вариант симплекс-таблицы, в котором помимо столбцов, соответствующих не базисным переменным, добавлены столбцы, соответствующие базисным переменным с нулевыми элементами, за исключением тех, которые стоят на пересечении строк и столбцов с одинаковыми номерами базисных элементов, равных единице.

Симплекс-таблица такого типа называется полной или расширенной в отличие от сокращенной симплекс-таблицы примера 16-2.