17-3. Классические методы определения экстремума функции
а) Задача на абсолютный экстремум
Если непрерывная функция n переменных n = (x1,...,xn) F(х) имеет в точке хопт максимум, то существует ε > 0 такое, что для всех ч из ε-окрестности точки хопт
F(x)≤F(xопт)
или
F(x)-F(xопт)≤0.
Выберем два вида приращения xj вдоль j-й координаты
Δxj=xj-xjопт>0,
Δxj=xj-xjопт<0.
Тогда
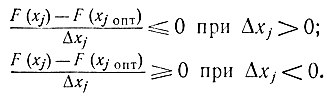
Переходя в этих соотношениях к пределу при Δxj→0, получаем:
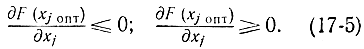
Из этих соотношений следует, что
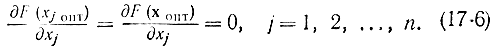
Аналогичное соотношение можно получить для случая минимума функции. Таким образом, доказана необходимость условий (17-6) для достижения в точке хопт максимума или минимума функции F(х), т. е. если имеется экстремум, то условия (17-6) удовлетворяются. Но равенство нулю всех производных в точке хопт еще не обеспечивает существования в ней экстремума, т. е. условия (17-6) не являются достаточными. Геометрически это означает, что в случае нулевой производной от функции одной переменной может иметь место точка перегиба, а не максимум (или минимум), а в случае функции двух переменных - седловая точка, а не экстремум и т. д. Поэтому точки хопт, в которых выполняются соотношения (17-6), называются стационарными.
Заметим, что условие (17-6) удалось получить благодаря возможности придавать переменной х приращения двух знаков, откуда и возникли два неравенства (17-5). Если допустимая область значений х ограничена неотрицательными значениями х≥0, то внутри области, где х > 0, справедливость условия (17-6) сохраняется, так как там допустимы приращения обоих знаков. На границе области х ≥ 0, где х = 0, допускается только положительное приращение Δх > 0, можно говорить только об односторонней производной, и из (17-6) следует следующее необходимое условие максимума:
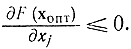
Необходимое условие минимума на границе области хj = 0 запишется в виде
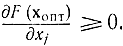
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'