б) Задача на условный экстремум

При определении условного экстремума функции, когда требуется определить максимум (или минимум) функции F(х) при ограничивающих условиях:

т. е.

используется также метод множителей Лагранжа, который, так же как в случае классического вариационного исчисления (гл. 11), заключается во введении функции Лагранжа

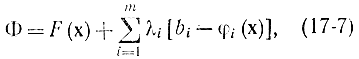
где λ_i - неопределенные множители Лагранжа.

Полагая, что функция является частным случаем функционала, или применяя методы, аналогичные использованным в гл. 11 (§ 6), получаем, что необходимые условия экстремума находятся прямым дифференцированием соотношения (17-7) и записываются в виде

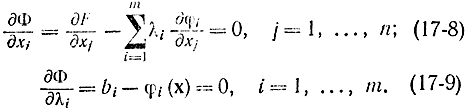
Если ввести в рассмотрение векторы

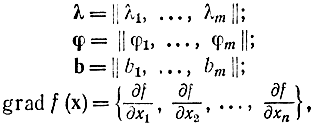
соотношения (17-8) и (17-9) перепишутся как

где равенство нулю векторов понимается покомпонентно.

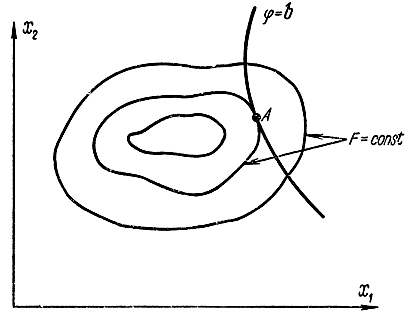
Рис. 17-6. Пояснение к задаче на условный экстремум

В случае n = 2 и m = 1 геометрическая задача об отыскании условного экстремума сводится (рис. 17-6) к отысканию точки касания А кривой φ = b к одной из кривых постоянного уровня F = const.