а) Алгоритм

Для удобства изложения представим все переменные в виде 2N - мерного вектора

Можно поставить в соответствие каждому вектору z вектор z^-, определяемый соотношением

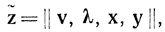
такой, что

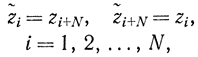
и

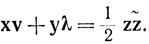
С помощью этих векторов условия (17-49) и (17-50) запишутся в виде

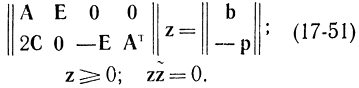
Исходя из некоторого допустимого базисного решения системы (17-51), совершим последовательность симплексных преобразований, с помощью которых будем уменьшать выпуклую функцию

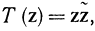
пока не достигнем значения Т = 0. Симплекс-метод в данном случае аналогичен использованному в линейном программировании, только усложняются правила выбора включаемых в базис переменных из-за нелинейности функции Т (z).

Допустим, имеется некоторое допустимое базисное решение системы (17-51). Симплекс-таблица в данном случае должна задавать входящие в базис переменные zg как функцию от N не базисных переменных z_vh = t_h, не входящих в базис

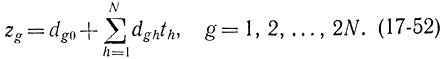
Эту запись можно использовать и для не базисных переменных из числа z_g. Для этого симплекс-таблица дополняется строками, все элементы которой, кроме одного, равного единице, равны нулю. В этих строках для не базисной переменной z_g = t_j будет d_gh = 0, h≠ j, a d_gj = 1. Нумерация всех переменных z_g базисных и не базисных дается от g = 1 до g = 2N.

Функциональную зависимость (17-52) можно записать в векторном виде:

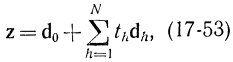
где d_h, - h-й столбец симплекс-таблицы. При не базисных переменных t_h = 0 формула (17-53) перепишется в виде

и

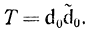
Включим в базис переменную t_j равнявшуюся нулю, сделав ее положительной (t_j = θ ≥ 0) и сохранив за остальными не базисными переменными t_h (h≠j) нулевые значения. После этого вектор

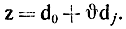
Увеличивать переменную t_j можно до тех пор, пока некоторая j-я из базисных переменных не обратится в нуль. Эта j-я переменная определяется из условия

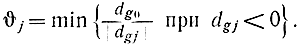
Положив t_j = θ_j, получим новое базисное решение, в котором вектор z принимает значение

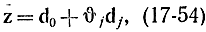
а величина Т соответственно

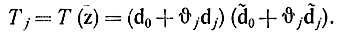
Так как

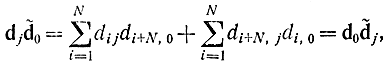
то

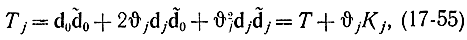
где

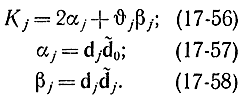
Очевидно, что правило включения в базис новой переменной должно быть таким, чтобы K_j<0, так как при этом уменьшается значение Т. Если отрицательных чисел K_j несколько, выбирается то, которому соответствует наименьшее отрицательное произведение θ_jK_j. Величины β_j, представляющие собою вторые производные от T_j по t_j = θ_j, в силу выпуклости функции Т всегда неотрицательны. Поэтому величина K_j может быть отрицательна только за счет α_j. В данном случае для тех j, для которых α_j<0, необходимо проверять, уменьшает ли базисное решение, в которое включены переменные t_j, значение функции Т. В этом состоит отличие от линейного программирования, при котором функция цели в силу линейности монотонно уменьшается при отрицательной первой производной α_j, и достаточно проверять только знак α_j. В случае квадратичной выпуклой функции цели Т исследования первых производных может быть недостаточно, так как эта функция может принимать экстремальное значение на отрезке, соединяющем старое и новое базисные решения.

Может быть и так, что K_j > 0 для всех j, хотя Т > 0. На рис. 17-11 пунктиром изображены линии равных значений функций цели Т и сплошными линиями - многогранник допустимых значений, определяемый соотношениями (17-51). Вершины соответствуют базисным решениям, а симплексное преобразование - переходу к соседней вершине. Для этого примера переход из точки Р₁ в Р₂ и Р₆ приводит к увеличению функции цели, хотя Р₁ не является глобальным минимумом. В данном случае метод Баранкина и Дорфмана в изложенном выше плане неприменим. Приходится идти на временное увеличение функции T, включая в базис переменную с положительным значением K_j и пытаясь пробиться через эту "мертвую зону".

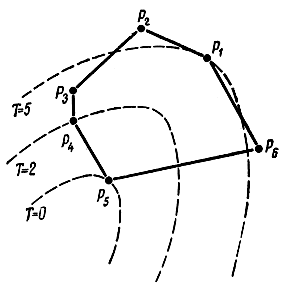
Рис. 17-11. Пояснения к методу Баранкина и Дофрмана

При дальнейшем развитии этого метода, реализованного в методе Франка и Вульфа, удается избавиться от этого недостатка.