б) Вычислительная схема

Исходный базис можно найти, использовав метод вспомогательных переменных, применяемый в линейном программировании (см. гл. 16), постепенно сводя эти переменные к нулю. Последовательность метода такова, что после определения допустимого базисного решения приступают к минимизации функции цели, для чего строят симплексную и дополнительную таблицы в виде табл. 17-1.

Таблица 17-1

В отличие от стандартной симплекс-таблицы здесь добавлена таблица для дополнительных переменных α₀, α_j, β_j, θ_j, K_j, которые вычисляются по следущим формулам:

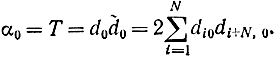
При α₀ = 0 сразу получаем оптимальное решение. В противном случае дополнительно находим:

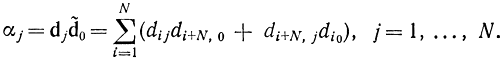
Далее для j, для которых α_j< 0, определяются

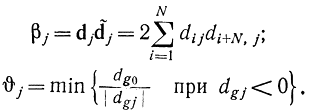
Для определения элемента j вычисляются

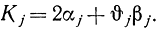
В качестве заменяющего столбца Выбирается такой, для которого отрицательное произведение θ_jK_j наименьшее. Элемент d_gj, по которому определено 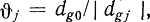, становится опорным, и из базиса удаляется соответствующая ему g-я переменная (заменяющая строка), которая встает на место переменной заменяющего столбца. Затем все элементы заменяющего столбца делятся на опорный, который при этом становится равным единице. Тем самым получаем заменяющий столбец с новыми элементами. Для получения остальных столбцов новой таблицы из соответствующих столбцов старой вычитаем уже построенный заменяющий столбец, умноженный на элемент, стоящий на пересечении преобразуемого столбца старой таблицы и заменяющей строки.

Описанный выше процесс формирования новой симплекс-таблицы полностью аналогичен такому процессу в линейном программировании и определяется в соответствии с формулой, которая получается из соотношения (17-51),если выразить переменную t_j, вводимую в базис, через остальные переменные. Допустим что опорный элемент стоит на пересечении i-й строки и j-го столбца:

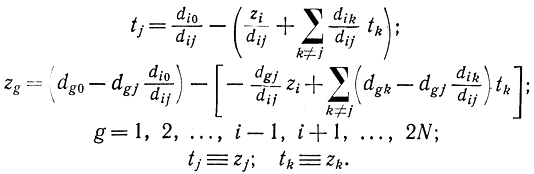
Первое соотношение соответствует делению элементов заменяющего столбца на опорный элемент и определяет новую (вводимую) строку. Второе соотношение определяет остальные строки или столбцы. Элементы нового вводимого столбца (соответствующего новой не базисной переменной z_i) формируются по тому же правилу, только в качестве элементов старого столбца берутся нули. Новая таблица подвергается такой же серии преобразований, как и старая. Процесс продолжается до тех пор, пока Т не примет нулевого значения. Однако можно еще улучшить процедуру вычислений, если сначала определить в соответствии с формулой (17-54) первый столбец таблицы 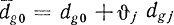и по d_g0, пользуясь формулой (17-57), вычислить α₀. Если α₀ = 0, то новое базисное решение оптимально, и мы сэкономили на одном симплекс-преобразовании.

Пример 17-1. Минимизируем функцию Q = -6х₁ + 2х²₁ - 2x₁х₂ + 2х²₂ при ограничениях x₁ + х₂ ≤ 2, х₁ ≥ 0, х₂ ≥ 0. Здесь

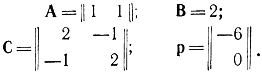
Запишем условия Куна - Таккера (17-51) для данного примера:

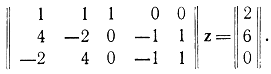
Найдем допустимое базисное решение данной системы уравнений, используя дополнительные переменные

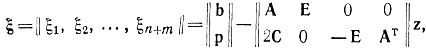
и вспомогательную функцию цели 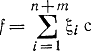с применением симплекс-метода. Исходная симплекс-таблица запишется в виде табл. 17-2.

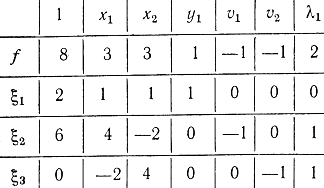
Таблица 17-2

Таблица 17-3

Затем получим последовательность симплекс-таблиц (табл. 17-3, 17-4, 17-5).

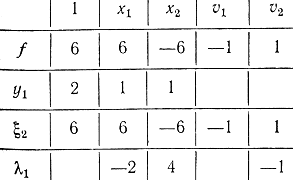
Таблица 17-4

Таблица 17-5

Согласно соотношениям (17-51), (17-56) - (17-58) и табл. 17-1, 17-5 составим следующую последовательность симплекс-таблиц (табл. 17-6, 17-7).

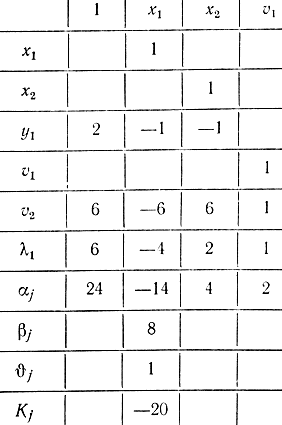
Таблица 17-6

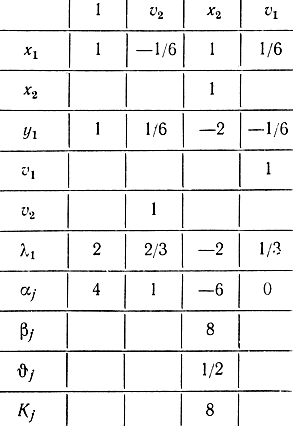
Таблица 17-7

Вычисляя предварительно на каждом шаге значение 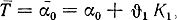можно избежать вычисления следующей последней таблицы.

В данном случае на следующем шаге значение функции согласно соотношению (17-55)

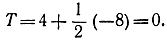
Следовательно, осталось вычислить оптимальные значения компонент вектора. Итак.

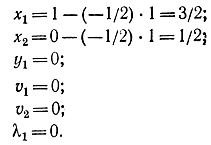
Оптимальное значение функции Q = -11/2.