17-8. Градиентные методы

В я-мерном пространстве поверхности

представляют собой концентрически расположенные эллипсоиды с центром в точке

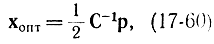
которая и является решением задачи квадратичного программирования

при условии соблюдения допустимых ограничений. Вектор-градиент функции (17-59)

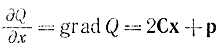
всегда перпендикулярен к поверхности (17-59), точнее, ко всем векторам; лежащим в плоскости, касательной к этой поверхности. В этом нетрудно убедиться, если записать уравнение (17-59) в виде дифференциального

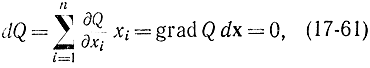
которое означает, что дифференциал равен нулю, если равно нулю скалярное произведение grad Qdx. Координаты точки оптимума (17-60) определяются из уравнения

Градиентный метод заключается в движении из некоторой начальной точки х°, лежащей на поверхности Q = const, по кривой, ортогональной к этой поверхности и определяемой уравнением

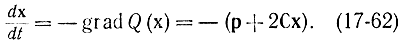
Если имеется задача нелинейного программирования

то для выпуклых функций Q (х) и области допустимых значений геометрически градиентный метод может быть иллюстрирован с помощью рис. 17-12. В случае, изображенном на этом рисунке, максимум достигается в точке, лежащей на кривой ψ₃ = 0, в которой кривая Q (х) = const касается кривой ψ₃ = 0.

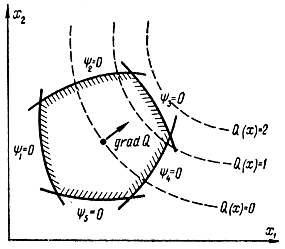
Рис. 17-12. Пояснение к градиентному методу в нелинейном программировании

Общая характеристика дискретных градиентных методов. Непрерывные или дифференциальные методы малопригодны для расчетов на ЦВМ. Поэтому предпочтение оказывают дискретным или пошаговым градиентным методам.

Первый метод Эйлера, применяемый, в отсутствие ограничений, заключается в замене дифференциального уравнения (17-62), определяющего непрерывный градиентный метод, разностным уравнением. Если обозначить

то уравнение (17-62) можно записать в виде

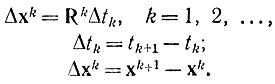
Другим дискретным градиентным методом является метод сопряженных градиентов. В этом методе [Л. 96] поиск точки х_опт начинается из некоторой точки х⁰ в направлении s⁰. При этом решают уравнения типа (17-61). Очередное приближение определяют из формулы

где

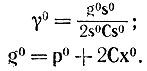
Очередное направление s¹ выбирают сопряженным предыдущему, т. е. удовлетворяющим уравнению

На k-м шаге s^k выбирают сопряженным s⁰, s¹,...,s^k-1, т. е.

Далее формируют

где

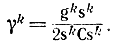
Можно доказать, что этот алгоритм приводит к экстремуму при отсутствии ограничений за конечное число шагов r≤n. Если первый шаг сделан вдоль координатной оси, то следующий делается перпендикулярно ей при условии, что С - единичная матрица, т. е. поверхность функции цели представляет собою часть сферы, причем таких направлений может быть (n - 1) (рис. 17-13, а). В этом случае метод сопряженных градиентов напоминает метод по координатного спуска, однако в последнем движение происходит вдоль той координаты, для которой значение производной максимально. Если матрица С - не единичная, то в соответствии со значениями ее элементов происходит деформация пространства (или плоскости при n = 2) значений функции цели, и угол между направлением последующего и предыдущего шагов становится не равным 90°, а определяется характером и степенью деформации пространства, т. е. траектория поиска как бы вписывается в рельеф (рис. 17-13, б). Величина k-го шага в соответствии с числителем g^ks^k формулы (17-64) определяется углом между направлением градиента функции цели в k-й точке и направлением k-то шага. Знаменатель формулы (17-64) принципиальной роли не играет и просто нормирует величину шага в зависимости от длины векторов s^k. Все векторы s^k, сопряженные с s^j (j = 0,1,..., k - 1) и имеющие начало в точке x^k, образуют( n - k)- мерное линейное подпространство, содержащее в себе центр эллипсоидов Q = const. При наличии ограничений ψ_i(х) ≤ 0 (i = 1, 2,..., m) эта точка может вообще не лежать в допустимой области. В этом случае точка х_опт будет лежать на пересечении некоторых гиперплоскостей a_ix = b_i ограничивающих допустимую область. Обозначим этот геометрический образ через D. Он имеет размерность r, где 0 ≤ r ≤ n - 1, и пересекает при r > 1 поверхность Q (х) = const по эллипсоиду размерностью r-1, центр которого и будет искомым оптимумом. Если известно заранее, что х_опт лежит в многообразии D, то, выбирая очередное s^k в соответствии с формулой (17-63) при условии, что s^k ∈ D, можно за конечное число шагов достигнуть оптимума, не выходя из многообразия. Если при определении x^k+1 встретится какое-нибудь новое ограничение, то это означает, что необходимо изменить D, т. е. исходное многообразие не содержало х_опт. Очевидно, что за конечное число шагов можно достичь правильного многообразия и внутри его оптимальной точки.

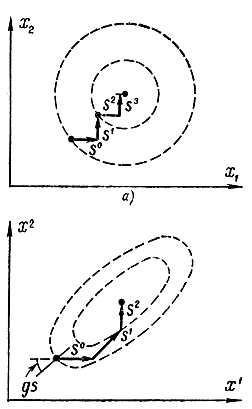
Рис. 17-13. Пояснение к методу сопряженных градиентов

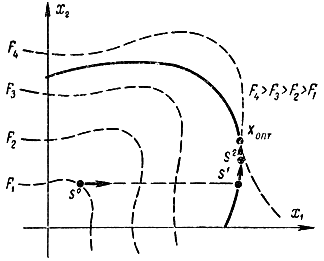
Рис. 17-14. Пример дискретного градиентного метода при ограничениях

В дискретных градиентных методах при ограничениях от k-й точки х^k двигаются в направлении градиента или, если не позволяют ограничения, в направлении вектора s, образующего с направлением градиента острый угол s grad F (x^k) > 0, до тех пор пока на этой прямой не будет достигнут максимум или движение будет невозможно (рис. 17-14). Одна группа методов (Зойтендейка) очередное (k + 1)-е направление движения определяет таким образом, чтобы скалярное произведение s grad F было максимально при выполнении условия требующего, чтобы при движении из точки x^k в направлении s траектория в достаточно малой окрестности точки x^k не выходила из допустимой области, т. е. эти методы связывают определение направления очередного шага с решением некоторой экстремальной задачи Другая группа методов (например, Розена) этого не требует, но она связывает выбор вектора s с его расположением в некотором линейном многообразии размерностью, меньшей n. В классическом методе Розена градиент проектируется на границу допустимой области размерностью, меньшей всего пространства.