17-9. Метод допустимых направлений Зойтендейка
Предполагается, что задана вогнутая функция цели Q, необязательно квадратичная, с непрерывным градиентом
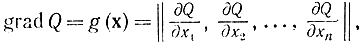
и требуется определить максимум этой функции при ограничивающих условиях
aix≤bi, i=1,2,.,...., m. (17-65)
Необходимо так определить направление перехода из точки хk в точку хk+1 = xk + γsk, чтобы новая точка при достаточно малом γ > 0 принадлежала области допустимых значений G, определяемой соотношениями (17-65). Необходимым и достаточным условием соблюдения этого требования является следующее:
aisk≤ для всех i ∈ S, (17-66)
где S - множество всех индексов i, для которых
aixk = bi (17-67)
т. е. это означает, что множество S соответствует границе допустимой области, достигнутой на предыдущем шаге, а условие (17-66) означает, что последующий шаг направлен внутрь и по границе области допустимых значений.
Направления, удовлетворяющие условиям (17-66) и (17-67), называются допустимыми.
Второе требование к выбору направления очередного шага заключается в том, чтобы функция цели увеличивалась вдоль выбранного направления хотя бы для малых γ, что обеспечивается неравенством
skg(xk)>0. (17-68)
Направления, удовлетворяющие условию (17-68), называются подходящими. Из допустимых и подходящих направлений выбирается некоторое частное направление с помощью условий нормализации, которыми и отличаются различные градиентные методы.
Процедура определения длины очередного шага γk при определенном sk во всех методах одинакова, а именно, определяется такое значение параметра γ', при котором луч "протыкает" область допустимых значений G, определяемую соотношением (17-65), или такое значение γ", при котором Q достигает максимума, т. е.
skg(xk + γ"sk) = 0, (17-69)
причем γ' и γ" могут быть бесконечно большими. После этого длина очередного шага определяется из соотношения
γk = min(γ', γ"). (17-70)
При бесконечно большом значении γk функция цели неограниченна. Если γk конечна, очередная точка вычисляется по формуле
xk+1=xk+γksk
Метод Зойтендейка решает на каждом шаге частные небольшие линейные и нелинейные вспомогательные программы, в которых может с успехом применяться симплекс-метод. Метод применим не только к квадратичным функциям цели и линейным ограничениям. Он не дает сходимости за конечное число шагов, однако если добавить условия сопряженности, то такая сходимость обеспечивается. Сформулируем вспомогательные программы Зойтендейка. Их идея заключается в том, что новое направление sk ищется оптимальным в том смысле, чтобы функция цели не просто увеличивалась, что обеспечивается соотношением (17-68), а увеличивалась за каждый шаг максимальным образом при определенных условиях, т. е. требуется найти sk, такое, что
gs = max, где g = g(xk)
при ограничениях
ais≤0 для i ∈ S (17-71)
и одном из пяти дополнительных нормирующих условий:
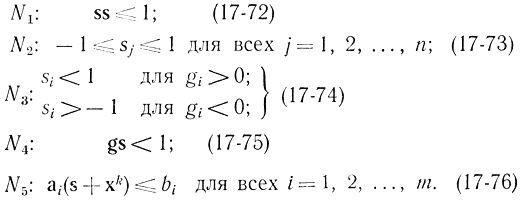
Следует заметить, что условие (17-71),справедливое для подмножества индексов i ∈ S, содержится в соотношении (17-71).
Условия нормализации необходимы для ограничения величины sk, так как иначе величину gs можно сделать сколь угодно большой при условии существования допустимого направления, для которого gs > 0. Если некоторые из ограничений исходной программы (17-73) имеют знак строгого равенства, то в соответствующих соотношениях (17-66) также должен стоять знак равенства, т. е. ais = 0. Можно ввести другие условия нормализации, и тогда получится новый градиентный метод.
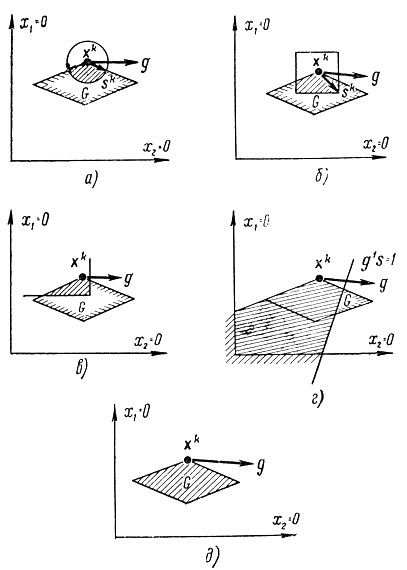
Рис. 17-15. Пояснение к методу Зойтендейка
Условие (17-72) ограничивает квадрат модуля вектора s. Условно это ограничение представлено на рис. 17-15,а в виде окружности. Ограничения (17-73) определяют куб допустимых значений вектора направления k-го шага sk, который может быть направлен в одну из вершин куба (рис. 17-15,6). Условие (17-74) для случая gi > 0 представлено на рис. 17-15,в. Допустимая область векторов sk на этом рисунке ограничена двумя лучами, пересекающимися под прямым углом. В случае нормирующего условия (17-75) область допустимых значений векторов sk лежит по одну сторону от прямой gs = 1 и не ограничена. Эти условия носят несколько более сложный характер, но очевидно, что вся допустимая область х является приемлемой с точки зрения выбора очередного шага, т. е. конец вектора sk может лежать в любой точке этой области (рис. 17-15, г), так как вектор sk складывается с вектором xk, и их сумма не должна выходить за пределы допустимой области значений х. Соотношения (17-76) допускают выбор сколь угодно больших отрицательных значений si т. е. область допустимых значений s не ограничена. Оказывается, что ограничения (17-72) приводят к нелинейным, а ограничения (17-73) и (17-74) - к линейным программам.
Пример 17-2. Рассмотрим случай с нормирующими условиями (17-76) при квадратичной функции цели Q = рх - хСх (С положительно полуопределена),
g (xk) = p - 2Cxk = gk. (17-77)
Длину очередного шага определим из соотношения
γk = min (γ' γ"),
где
γ"=gsk/2(sk)Csk. (17-78)
Формулу (17-78) получим из (17-69), учитывая (17-77),
skg (хk + γ"sk) = sk [р - 2C(xk + γ'sk)] = skp-sk2Cxk - s2Cγ'sk = skg (xk) - s2Cγ'sk = 0.
Физически это означает, что очередной шаг выбирается таким образом, чтобы сразу попасть в точку экстремума. В случае (17-76) величина, обеспечивающая "протыкание" лучом области допустимых значений, всегда равна единице, так как в соответствии с формулой (17-76) сам вектор sk выбирается так, чтобы "проткнуть" эту область.
Рассмотрим задачу, решенную в примере 17-1. Максимизируем квадратичную форму Q = 6x1 - 2х21 + 2х1х2 - 2х22 = max при ограничениях х1 + х2 ≤ 2, х1 ≥ 0, х2 ≥ 0.
Здесь
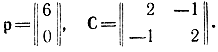
В качестве исходной точки возьмем х0 = || 0,0 ||. Вопрос о выборе этой точки требует специального обсуждения, на котором здесь мы не останавливаемся. Начальное значение градиента
g(x0) = g0 = ||6, 0||.
- Первая вспомогательная программа в соответствии с нормализацией (17-76) заключается в том, чтобы максимизировать выражение g0s = 6s1 = max при ограничениях
s1 + s2 ≤ 2; s1 ≥ 0, s2≥0 (17-79)Это - задача линейного программирования. Для ее решения введем вспомогательную переменную ух и составим симплекс-таблицу (табл. 17-8). Уже на следующем шаге с помощью оптимальной симплекс-таблицы (табл. 17-9) придем к оптимальному решению.

Таблица 17-8Чтобы из табл. 17-9 получить оптимальное решение, необходимо значения координат, соответствующих не базисным переменным, приравнять нулю (sx = 0), а остальные переменные (sx = 2) взять из таблицы: s0 = || 2, 0 ||. Далее, g0s0 = 12, s0Cs0 - 6, γ" = 12/2-6 - 1, Так как при условиях (17-76) γ' - 1, то γ0 - min (γ', γ") = 1. После первого шага координаты следующей точки определятся как
Таблица 17-9х1 =x0+γ0s0 = || 2, 01|;g1 = р - 2Cx1 = ||- 2, 4||.Поскольку γ0 = γ", используем условие сопряженности s0Cs = 0, а именно,4s1-2s2 = 0, (17-80)т. е. добавим условие (17-80) к ограничениям (17-79). Можно показать [Л. 96], что при вычислениях удобно пользоваться заменой s → t в соответствии с формулой t = xk + s. Это в ряде случаев позволяет применить сокращенный метод таблиц. Подставим t1 = х1 + s. Тогда дополнительное условие (17-80) запишется в виде 4t1 - 2t2 = 8. - Во второй вспомогательной программе требуется найти максимум g1x1 = -2t1 + 4t2 при условиях
t1t2y1=2, y1≥04t1-2t2+y2=8, y2=0t1≥0, t2≥0Составим первую и вторую симплекс-таблицы второго шага (табл. 17-10, 17-11).
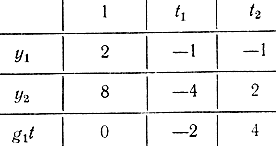
Таблица 17-10После второго шага имеем: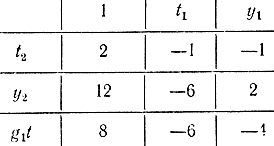
Таблица 17-11Поскольку γ0 = γ"; γ1 = γ", для третьего шага к ограничениям (17-79) необходимо добавить уже два дополнительных условия, соответствующих s0Cs = 0 и s1Cs = 0, а именно, 4s1 - 2s2 = 0; -6s1 + 6s2 = 0. Теперь подставим t2 = х2 + s и получим задачу третьего шага.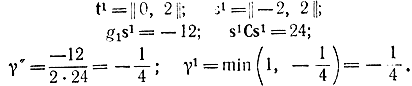
- В третьей вспомогательной программе требуется найти максимум g2t2 = -5t1 + 7t2 при условиях
t1t2y1=2, y1≥0, t12≥04t1-2t2+y2=9, y2=06t1-6t2+y=12, y3=0Решение находим аналогично предыдущему:Выбираем γ2 = γ" = 2/5. После третьего шага х3 = || 3/2, 1/2 ||. Поскольку g3 = || 1, 1 ||, к ограничениям (17-79) следует добавить уже три дополнительных условия
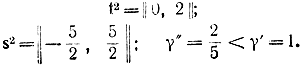 соответствующие условиям сопряженности
соответствующие условиям сопряженности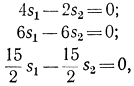 s0Cs = 0;s1Cs = 0;s2Cs = 0.Подставим t3 = x3 + s и получим задачу четвертого шага.
s0Cs = 0;s1Cs = 0;s2Cs = 0.Подставим t3 = x3 + s и получим задачу четвертого шага. - На четвертом шаге необходимо найти максимум g3t3 = t1 + t2 = max при условиях:
Решение четвертой вспомогательной программы запишется как
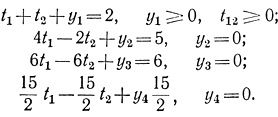 откуда решение искомой квадратичной программы найдется в виде х3 = || 3/2, 1/2 || и
откуда решение искомой квадратичной программы найдется в виде х3 = || 3/2, 1/2 || и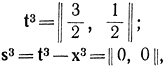
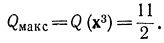
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'