Глава восемнадцатая. Целочисленное программирование

Математическая формулировка задач целочисленного программирования аналогична задачам нелинейного программирования:

Однако специфика задач целочисленного программирования заключается в том, что переменные х_j и функции F(х), ψ_j(х) могут принимать только дискретные значения. Нормировкой или специальными преобразованиями в подавляющем большинстве случаев можно свести эти дискретные значения к целочисленным.

В общем случае целочисленными могут быть не все, а части переменных и функций. Иногда целочисленное программирование называется дискретным программированием [Л. 97]. Однако, как уже указывалось выше, при полном рассмотрении всех методов оптимизации этот термин оказывается занятым в другом смысле. Если все функции F (х) и ψ_i(х) в задаче (18-1) линейные, то имеет место линейная задача целочисленного программирования. Методы решения таких задач получили наибольшее распространение. Очевидно, что могут встречаться задачи с целочисленными переменными x_j и функциями F(x) и ψ_i(х) и целочисленными переменными и непрерывными функциями (рис. 18-1). Как правило, именно этот последний случай рассматривается в большинстве руководств. Кроме того, встречаются задачи частично и полностью целочисленные в зависимости от того, часть или все переменные x_j принимают целочисленные значения. Как уже отмечалось, допустимые дискретные значения, входящие в множество, могут быть даже не целочисленными. В частности, это множество может быть бесконечным, конечным или даже состоящим всего из двух значений: 0 и 1. В этом случае имеет место целочисленное программирование с булевыми переменными, методы которого в значительной мере перекрываются логическим синтезом конечных автоматов.

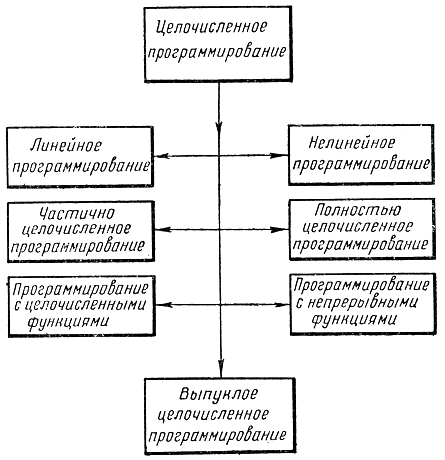
Рис. 18-1. Классификация задач целочисленного программирования

Следует заметить, что методы целочисленного программирования значительно отличаются от методов оптимизации, рассмотренных в первых главах данной части, и по существу своему относятся к дискретной математике. Они не обладают таким единством, как методы вариационного исчисления, и в большинстве представляют собой набор частных приемов, пригодных для решения частных задач. Однако их актуальность требует их дальнейшего развития и совершенствования, так как наиболее важные прикладные задачи типа оперативно-календарного планирования сводятся к задачам целочисленного программирования.

Со значительными оговорками все методы решения задач целочисленного программирования можно разделить на четыре группы (рис. 18-2): методы отсечения, комбинаторные, приближенные и другие методы, которые нельзя отнести ни к одной из трех первых групп [Л. 89, 97].

Первая группа использует процедуру линейного программирования для последовательности задач, в которые постепенно вводятся линейные ограничения, и тем самым реализуется процесс правильного отсечения. Основу всех методов этой группы составляют три алгоритма Гомори и их модификации.

Большинство комбинаторных методов не использует процедуру симплекс-метода, а достигает сокращения поиска оптимальных значений анализом исходного множества.

С развитием прикладных разделов кибернетики все большее значение приобретают приближенные методы решения задач оптимизации, которые для частной исходной постановки обеспечивают эффективное отыскание приближенного решения за значительно меньшее число шагов. Здесь широко применяются случайные методы поиска, аналогичные градиентным и прямым, а также специальные методы, использующие эвристический подход.

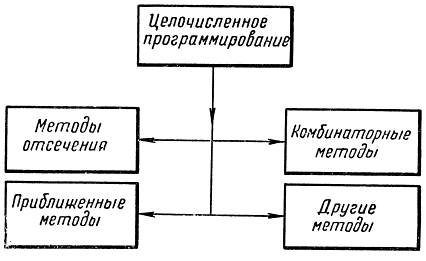
Рис. 18-2. Классификация методов решения задач целочисленного программирования

Следует напомнить, что целочисленные методы оптимизации отличаются от дискретных прямых методов аналитической постановкой задачи вида (18-1) и доказательством сходимости, оптимальности и т. д. Дискретное динамическое программирование по-прежнему успешно применяется для решения задач целочисленного программирования и в приведенной на рис. 18-2 классификации содержится в разделе комбинаторных методов, так как по существу оно является направленным методом перебора. Значительно реже используется дискретный принцип максимума. Широкие возможности в части решения прикладных задач большой размерности открываются при использовании человеко-машинных методов оптимизации. Однако для эффективного их использования требуются развитые операционные системы ЦВМ, технические и программно-информационные средства общения человек - машина. По своей идеологии эти методы примыкают к лингвистическим с добавлением блоков эвристики, в качестве которых выступает человек при общении с ЦВМ.

Человеко-машинные методы еще недостаточно разработаны и поэтому в данном руководстве они подробно не рассматриваются.