Глава вторая. Общая методология нелинейного программирования. Гладко-выпуклые структуры

2.1. Особенности нелинейных задач. Классические условия экстремума

Приступая к изучению проблематики нелинейного программирования, обратим внимание на ряд обстоятельств, которые способствуют разрешимости конечномерных оптимизационных задач. Здесь можно, в частности, указать на:

- наличие только абсолютного (глобального) экстремума целевой функции, что устраняет необходимость дополнительных проверок результата решения;

- выпуклость области определения задачи и возможность выбирать значения x_j среди всех действительных неотрицательных чисел, что позволяет формировать условия существования экстремальных точек Х° или X^*;

- гладкость функций f(X), g_i (X), облегчающую применение аппарата классической математики для поиска оптимальных решений и для разработки новых подходов к задачам математического программирования.

Перечисленными свойствами обладают линейные задачи (см. гл. 1), но большинству нелинейных задач присущи такие особенности, которые затрудняют (а иногда делают невозможными) исследования общего характера. В этих условиях большое значение приобретают результаты, содержащие обоснованные и пригодные для практического использования рекомендации.

Проблема отыскания условного экстремума скалярной функции многих переменных была изучена еще Лагранжем, предложившим так называемый метод множителей применительно к задаче с ограничениями-равенствами g_i (X) = b_i, t = 1,....,m. Представляя большой самостоятельный интерес, этот метод позволил получить в более позднее время ряд обобщений, которые привели к разработке алгоритмов решения задач с неклассическими условиями (в первую очередь - задач выпуклого квадратичного программирования).

Изучение метода множителей Лагранжа удобно провести на следующем примере: дана целевая функция z = = f(x₁, х₂) и единственное ограничение g(x₁, х₂) = b, наложенное на рассматриваемые x₁, х₂ (требования не отрицательности и целочисленности x₁, х₂ отсутствуют); f(х₁, х₂) и g(x₁, х₂) принадлежат по крайней мере второму классу гладкости, а для g(x₁, x₂) = b верна теорема существования неявных функций; требуется получить необходимые условия, которым должна удовлетворять точка локального экстремума z в задаче: найти x₁, x₂→max{z = f (х₁, х₂)} при g(x₁, x₂) = b.

В этой ситуации с помощью равенства g(x₁, x₂) = b можно представить х₂ как x₂ = φ(x₁) и прийти к выражению z = f[х₁, φ(x₁)] = h(x₁). Необходимость учета ограничения g(x₁, x₂) = b приводит к тому, что из всех точек плоскости х₁, х₂ интерес представляют лишь те, которые лежат на линии, определяемой уравнением x₂=φ(x₁) (рис. 2.1). Если в какой-либо из этих точек z достигает локального экстремума, то и h(x₁) достигает экстремума в некоторой точке x°₁ являющейся первой координатой Х°. Экстремум h(x₁) - локальный, но он не является условным, поскольку способ построения функции h(x₁) предусматривает учет исходного ограничения и никаких

дополнительных требований к х₁ предъявлять не нужно, Следовательно, величина х°₁ может быть найдена из уравнения [dh(x₁)/dx₁]_x⁰1 = 0.

Имея в виду равенства h(x₁) = f[x₁, φ]; dh/dx₁ = df/dx₁+df/dφ×dφ/dx₁, dφ/dx₁ = dg/dx₁(dg/dx₁)^-1, получаем

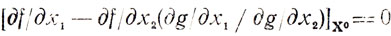
или [df/dx₁-λdg/dx₁)_x° = 0, где X - новое обозначение df/dx₂/dg/dх₂ (оно допустимо, если dg/dx₂ = 0), это дает df/dx₂-λdg /dх₂ = 0.

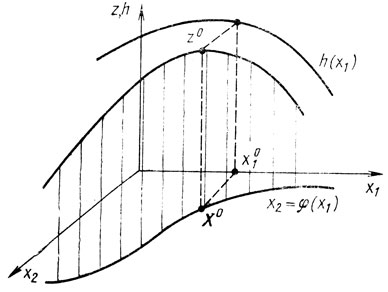
Рис. 2.1

Искомые необходимые условия существования Х° представляются теперь в виде уравнений

совместное решение которых относительно x₁, х₂, λ по-

зволит указать все точки Х°.

Главное удобство найденной формы записи состоит в том, что система (2.1) может быть получена более коротким и чисто формальным путем. Для этого достаточно составить выражение вида f(x₁, х₂) + λ[b - g(x₁, х₂)] = Φ(x₁, х₂, λ), а затем найти и приравнять

нулю частные производные ∂Φ/∂x₁, ∂Φ/∂x₂, ∂Φ/∂λ, считая x₁, х₂, λ, независимыми переменными. Функция Φ(x₁, х₂, λ) называется функцией Лагранжа, множитель X - множителем Лагранжа. Ниже приведен пример применения метода.

Пример: найти длину сторон ирямоугальннка с максимальней площадью S, вписанного в круг х²₁+x²₂≤r².

Решение: если x_1B и х_2В - координаты вершины рассматриваемого прямоугольника, то целевая функция S есть 4x_1Bx_2B; ограничение, которому должны удовлетворять переменные x_1В и х_2В, представляет собой уравнение окружности х²_1В+х²_2В = r²; dg/dx² = 2x_2B≠0; функция Лагранжа в данном случае имеет вид Φ(x_1В, x_2B, λ) = 4x_1Bx_2B + λ[r²-х²_1В-х²_2В]; приравнивание нулю ее производных дает

решая совместно эти три уравнения, получаем х°_1В = r/√2 , х°_2В = = r/√2,λ° = 2 (прямоугольник с S = S_max должен быть квадратом); полезно отметить, что решение задачи представлено в виде набора оптимальных значений x°_1B, х°_2B, λ°.

Выше был изучен частный вариант классической задачи математического программирования, для которого n = 2, m = 1. Существует обобщение метода множителей на случай произвольного числа переменных n и ограничений-равенств m (m<n). Здесь функция Лагранжа есть

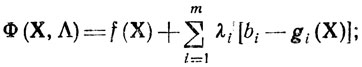
символами X и Λ обозначены векторы (x₁, х₂, ...,х_n) и (λ₁, λ₂,...,λ_m). Необходимые условия локального экстремума представляются как

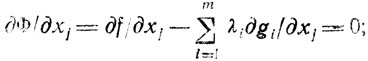(2.2)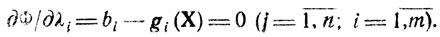

Таким образом, для отыскания точек Х° приходится решать систему m+n уравнений вида (2.2), причем необязательно, чтобы любое допустимое решение системы (2.2) доставляло относительный условный экстремум функции f(X), но каждая точка, в которой такой экстремум достигается, должна удовлетворять условиям (2.2).

Преимущество рассмотренного метода в том, что можно не учитывать взаимную зависимость переменных; недостатком является необходимость решения громоздких уравнений (2.2), что далеко не всегда просто. Разработанный применительно к классической постановке задачи этот метод, как выяснилось, допускает обобщение на случай ограничений-неравенств вида g_i(X)≤b_i, а также ∀x_j≥0, что позволяет использовать его модификации в решениях неклассических задач.

Прежде всего полезно выяснить, какую роль играют множители λ⁰_i (или λ^*_i) в решениях, получаемых из

(2.2). Иногда возникает вопрос: не лучше ли как-то разумно изменить ограничения и получить за счет этого заметный выигрыш в величине z^*, чем довольствоваться тем значением z^*, которое следует из решения задачи с исходными фиксированными ограничениями? Подобная ситуация часто встречается при варьировании характеристик систем с целью отыскания компромиссных сочетаний их полезных свойств.

Пусть найдена совокупность величин х^*₁, х^*₂, ... ,х^*_n, λ^*₁, λ^*₂, ...., λ^*_m, доставляющих целевой функции z = f(X) абсолютный экстремум z^* при определенных условиях задачи (предполагается, что использован метод множителей Лагранжа). В общем случае x^*_j (j = 1,....,n) и λ^*_i(i = 1,...,m) зависят от значений b_i (правые части строк-ограничений). Следовательно, и величина z^* должна зависеть от b_i (i = 1,...,m). Рассмотрим выражение

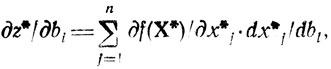(2.3)

допуская существование входящих в него частных производных в окрестности точки В = (b₁, b₂,..., b_m). Составим и обозначим через δ^*_ik аналогичную сумму

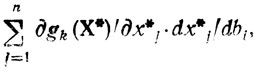
так что

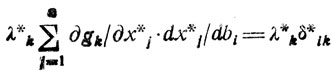
или

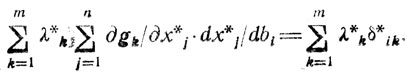(2.4)

Если теперь сложить почленно (2.3) и (2.4) и провести очевидные преобразования, то в полученном соотношении

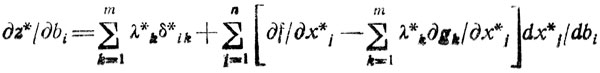
разность в квадратных скобках равна нулю (как производная функции Лагранжа в экстремальной точке). Обращаясь к выражению δ^*_ik и учитывая, что g_i(x^*₁, x^*₂, ..., x^*_n) = b_i, приходим к выводу: b^*_ik = 0 при i ≠ k. Таким образом, dz^*/db_i = λ^*_i, т. е. каждый множитель λ^*_i(i = 1,...,m) определяет "реакцию" значения z^* на изменение соответствующего параметра b_i. По величине λ^*_i можно судить о том, какое из ограничений задачи лучше всего изменить, чтобы получить максимальное приращение |z^*|.

Обратимся теперь к некоторым обобщениям метода множителей.