2.2. Возможные обобщения метода множителей. Седловая точка функции Лагранжа

Здесь будут обсуждены вопросы, относящиеся к использованию введенных выше понятий применительно к оптимизационным задачам, содержащим ограничения вида ∀x_j≥0 (j = 1,...,n) и g_i(X)≤b_i (i = 1,...,m). Главное внимание уделяется изучению особенностей функции Лагранжа Φ(Х, Λ) и связанных с ними условий существования экстремума.

Введем определение: точка Х°, Λ°, заданная своими координатами x°₁, х°₂, ..., х°_n, λ°₁, λ°₂, ..., λ°_m, является седловой для функции Φ(Х, Λ), если неравенства Φ(Х, Λ°) ≤ Φ(Х°, Λ°) ≤ Φ(Х°, Λ) выполнены для всех X, Λ из некоторой окрестности Х°, Λ°.

Это определение относится к локальной седловой точке, поскольку требование выполнить указанные в нем неравенства связано лишь с теми X, Λ, которые находятся "вблизи" Х°, Λ°. В том же смысле можно говорить и обо всех X, Λ, представляющих интерес в той или иной задаче; соответствующая седловая точка рассматривается как глобальная.

Анализ необходимых условий существования таких точек будет проведен в предположении, что часть переменных x_j, λ_i не имеет ограничения на знак, остальные же должны быть либо неотрицательными, либо не положительными; для конкретности ∀x_j=0, ∀λ_i≥0 при j = 1,...,s и i = 1,...,u; ∀x_j≤0, ∀λ_i≤0 при j = s+1,...,t и i = u+1,...,v; произвольный знак имеют x_j и λ_i при j = t+1,...,n, i = v+1,...,m.

Пусть точка Х°, Λ° является седловой для Φ(Х, Λ). Рассмотрим две группы производных, считая, что таковые существуют: ∂Φ/∂x_j, ∂Φ/∂λ_i. Поскольку Х°, Λ° определена как точка максимума Φ по X и минимума по Λ, производные ∂Φ/∂x_j, ∂Φ/∂λ_i должны обратиться в нуль при x_j = x°_j, λ_i = λ°_i, если нет ограничений на знак этих x_j, λ_i.

Таким образом, (∂Φ/∂x_j)_x°j = 0 для j = t + 1,..., n и (∂Φ/∂λ_i)λ°_i для i = v + 1,...,m.

Чтобы понять, как ведут себя рассматриваемые производные при i∈{1, 2, ..., v}, j∈{ 1, 2, ..., t}, достаточно выбрать переменную х_k с номером 1s (≤k≤ х_k≥0) и провести на ее примере необходимое исследование, считая все остальные переменные фиксированными.

Если Φ(X, Λ) как функция только х_k достигает максимума при х_k = х⁰_k > 0, то (∂Φ/∂x_k)_x⁰k = 0; но если x°_k = 0 (точка максимума Φ принадлежит границе области х_k ≥ 0), то можно ожидать либо (∂Φ/∂x_k)_x°k = 0, либо (∂Φ/∂x_k)_x°k Γ0 (рис. 2.2). Повторив подобные рассуждения применительно к другим x_j, λ_i нетрудно получить сводку необходимых условий существования Х°, Λ°;

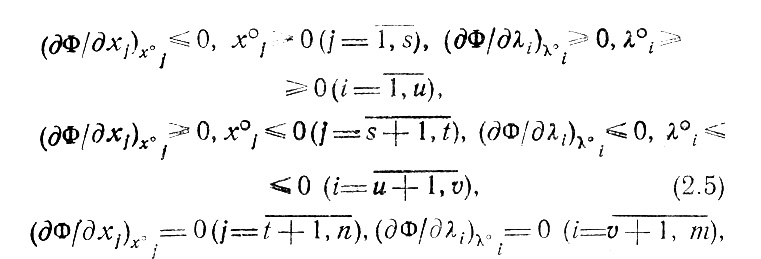
причем всегда х_j(∂Φ/∂x_j)_х°j = 0(j = 1, ..., n) λ°(∂Φ/∂λ_i)_λ°i (i = 1,...,m).

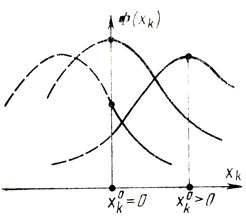
Рис. 2.2

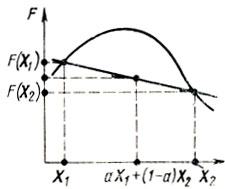
Рис. 2.3

Для анализа достаточных условий введем определение: некоторая функция F(X) называется выпуклой на интервале [Х₁, Х₂], если F[aX₁+(1-a)X₂]≤|aF(X₁) + (1-a)F(x₂) при 0<а<1 (рис. 2.3). В основе определения вогнутой на [Х₁, Х₂] функции лежит неравенство противоположного смысла, причем часто употребляются термины "выпуклая вниз", "выпуклая вверх".

Пусть Φ(Х, Λ) является выпуклой (вверх) по X для всех X из ε-окрестности Х°, т. е.

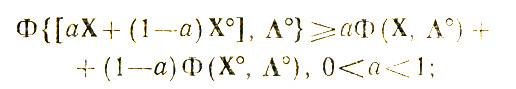
это значит (Φ{[аХ+(1-а)Х°], Λ°} - Φ(Х°, Λ°))/а≥Φ(X, Λ°)-Φ(Х°, Λ°). Выбирая ε таким, что Φ{[аХ + (1-а)Х°], Λ°} = Φ(Х°, Λ°) + а(Х - Х°) ∇_xΦ(Х , Λ°) (сохраняются линейные члены разложения в ряд Тейлора), получаем (X-Х°)-Φ(Х°, Λ°)≥Φ(Х, Λ°) - Φ(Х°, Λ°) или Φ(Х, Λ°)<Φ(Х°, Λ°) + ∇_xΦ(Х°, Λ°) × (X-Х°). Слагаемое (X-Х°)∇_xΦ(Х°, Λ°) интерпретируется, очевидно, как

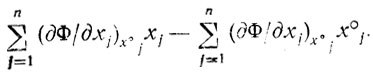
Если все эти соотношения рассматриваются при выполненных условиях (2.5), то

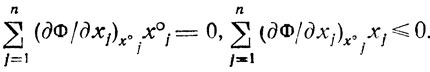
Следовательно, Φ(Х, Λ°)≤Φ(Х°, Λ°) + (неположительная величина) и тем более Φ(Х, Λ°)≤Φ(Х, Λ°). Таким образом, из (2,5) и предположения о выпуклости вверх Φ(Х, Λ) по X получено неравенство, присутствующее в определении седловой точки.

Считая теперь Φ(Х, Λ) выпуклой (вниз) по Λ вблизи Λ°, т. е. Φ{Х°, [аΛ+(1-а)Λ°]}≤аΦ(Х°, Λ) + (1-а)Φ(Х°, Λ°) при 0<a<1, нетрудно прийти к выводу: Φ(Х°, Λ)≥Φ(Х°, Λ°). Этим подтверждается достаточность общих условий (2.5) и требования "Φ(Х, Λ) должна быть выпуклой по X и вогнутой по Λ в окрестности Х°, Λ°" для существования "седла".