2.3. Оптимальные решения при ограничениях неравенствах. Теорема Куна-Таккера

Изученные особенности функции Φ(Х, Λ) позволяют сформулировать положения, относящиеся непосредственно к нелинейным задачам математического программирования. Пусть дана задача: найти

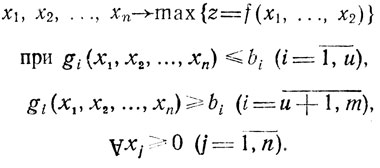(2.6)

Все предположения относительно z и g_i (i = 1,...,m), выдвинутые выше, сохраняются здесь полностью. Требуется получить условия существования решений, основанные на введенных понятиях.

Чтобы избежать неудобств, связанных с присутствием в (2.6) ограничений-неравенств и требований не отрицательности переменных x_j, представим (2.6) в эквивалентной форме

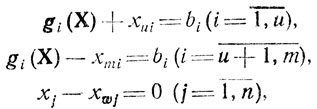(2.7)

где x_ui, x_mi, x_wj≥0 - вспомогательные переменные, позволяющие формально исключить знаки "≤, ≥", из (2.6). Для этого случая функция Лагранжа запишется как

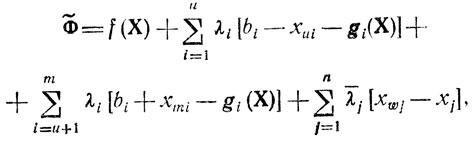
а необходимые условия, которым должны удовлетворять оптимальные x°_j, λ°_i, принимают обычный вид

Рассмотрим более подробно равенства (д∂Φ̃/∂x_j)° = 0 (j = 1,...,n). Их можно представить как

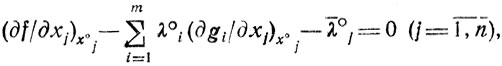(2.8)

собрав под знаком Σ производные по первых двух сумм выражения Φ. Ясно, что появление здесь слагаемого λ°_j есть следствие перехода от системы (2.6) к (2.7). Обратим теперь внимание на то, что в левую часть (2.8) входит выражение производной по x_j функции

т. е. функции Лагранжа в ее классическом виде (см. п. 2.1). Для составления Φ(Х, Λ) достаточно данных исходной задачи (2.6), поэтому естественно стремиться сформулировать такие условия существования экстремума f(X), которые включали бы только Φ(Х, Λ), а не Φ̃.

Обратим внимание на множитель λ̄°_j, связанный с о-й искусственной строкой (2.7) и обладающий свойством λ̄°_jx°_wj = 0. При x°_wj≥0 (или, что то же, при x°_j≥0) он обращается в нуль, и необходимые условия существования Х° (из рассматриваемых в данный момент) принимают вид

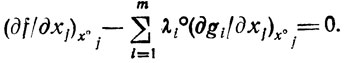
Далее, при х°_wj = 0 (это равносильно равенству x°_j = 0, так как x°_j-x°_wj = 0) соответствующий множитель λ̄°_j отличен, вообще говоря, от нуля. Его знак в этом случае определяется из следующих соображений: если правой части любой строки x_j-x_wj=0 дать отрицательное приращение, то область определения исследуемой задачи только расширится (произвольное значение х_j≥0 удовлетворяет и неравенству x_j≥b_wj, b_wj<0); величина z° при этом не уменьшится (всякое расширение U создает предпосылки для улучшения ожидаемых z°), т. е. dz°/db_wj≤0 или λ°_j≤0. Таким образом, при x°_j = 0 необходимые условия есть

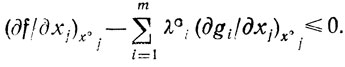
Обращаясь теперь к группе соотношений (∂Φ̃/∂λ_i,)_λ°i = 0 (i = 1,...,m) и применяя те же способы оценки знаков λ°_i, можно получить объединенную сводку искомых необходимых условий, которым должны удовлетворять оптимальные x°_j, λ°_i (j = 1,...,n; i = 1,....,m) в рассматриваемой задаче (2.6):

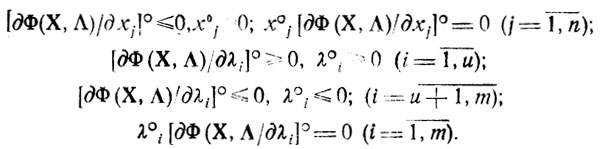(2.9)

Следует специально подчеркнуть, что соотношения (2.9) должны рассматриваться лишь тогда, когда существуют такие при которых ∂Φ/∂λ_i, т. е. g_i(X)<b_i (i = 1,...,u) g_i(X) > b_i (t = u+1,....,m); в противном случае возникает неопределенность выбора λ_i (нарушается условие регулярности ограничений (2.6), множество компонент Λ становится неограниченным), и равенства λ°_i(∂Φ/∂λ_i)° = 0 теряют смысл.

Очевидно, требования (2.9) полностью совпадают с (2.5) при Х≥0, причем соответствие результатов распространяется и на достаточные условия существования Х°, Λ°.

Пусть точка Х°, Λ°, удовлетворяющая (2.9), является седловой для Φ(Х, Λ); следовательно, должно выполняться неравенство

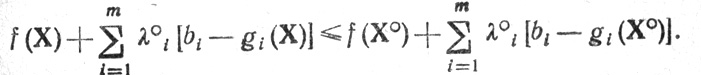
В силу (2.9) (сумма

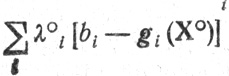
равна нулю, а каждое слагаемое суммы

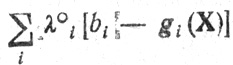
неотрицательно поскольку знаки разностей b_i-g_ш(X) в (2.6) и соответствующих λ°_i в (2.9) всегда совпадают. Таким образом, приходим к утверждению "f(X) + (неотрицательная величина) "f(Х°)" и тем более f(X)≤f(X°). Этим подтверждается достаточность исходного предположения.

Проведенный анализ свойств экстремума z в задаче (2.6) позволяет дать краткую формулировку теоремы Куна - Таккера: для того, чтобы экстремум функции f (X) был достигнут в точке Х°=(x°₁, х°₂, ..., х°_n) при условиях (2.6), необходимо и достаточно требовать существования таких (i = 1,...,u), λ°_i≤0 (i = u+1,....,m) при которых Х°, Λ° является седловой точкой функции (Х, Λ).

Заметим теперь, что теорема Куна - Таккера, отражающая роль седловой точки Х°, Λ°, может рассматриваться с более общих позиций, вне связи с предположениями о дифференцируемости Φ(Х, Λ).

Пусть, например, в задаче (2.6) отсутствуют требования существования производных df(X)/dx_j, dg_i(X)/dx_j и некоторая точка X^*, Λ^* является седловой для функции

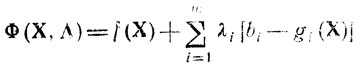
на множестве U, причем λ_i≥0 (i = 1,....,u), λ_i≤0, (i = u+1,....,m). Нетрудно убедиться, что эти условия являются достаточными условиями экстремума (в данном случае максимума). Действительно, из определения седловой точки (см. § 2.2) следует Φ(Х, Λ^*) ≤ Φ(Х^*, Λ^*) ≤ Ф(Х^*, Λ); правое неравенство есть

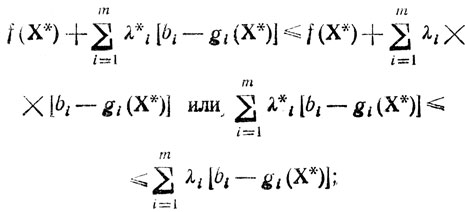
поскольку знаки λ_i^* совпадают со знаками соответствующих разностей b_i-g_i(X^*), и кроме того, рассматриваемое неравенство выполняется для всех допустимых λ_i (в частности, для ∀ λ_i=0 i=1,....,m), получаем

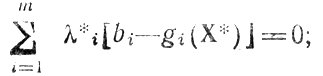
в этой ситуации левое неравенство принимает вид f(X) + (неотрицательная величина) f(X^*) или f(X)≤f(X^*), что и подтверждает оптимальность Х^*.

Т образом, использование производных функции Φ(Х, Λ) в ходе доказательств теорем о существовании экстремума совсем не обязательно, однако в инженерных задачах оно часто приводит к упрощениям расчетов.

В заключение полезно подвести некоторые итоги: исследована проблема обобщения классического метода множителей Лагранжа на случай ограничений вида g_i(X)≤bi и Х≥0 в задачах нелинейного программирования; показана возможность такого обобщения и изучены особенности функции Лагранжа Φ(Х, Λ) в точке относительного экстремума f(X); установлена связь между условиями существования точек Х° и Х°, Λ°, выраженная теоремой Куна - Таккера. Ниже дан пример непосредственного использования полученных результатов.

Пример: найти x₁, х₂ → max {z = -10(x₁-2)²-20(x₂-3)²} при x₁+x₂≤6, x₁-x₂≤1, 2x₁+х₂≥6, x₁/2-х₂≥-4; х₁, х₂ ≥ 0.

Решение: составим функцию Лагранжа в ее классическом виде (так, как это было бы в случае ограничений-равенств и отсутствия требований не отрицательности х₁, х₂):

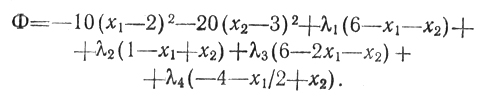
Из условий x°_j (Φ'_xj)_x°j = 0 (j = 1, 2) и λ°_i (Φ'_xj)_λ°i = 0 (i = 1,...,4) получаем

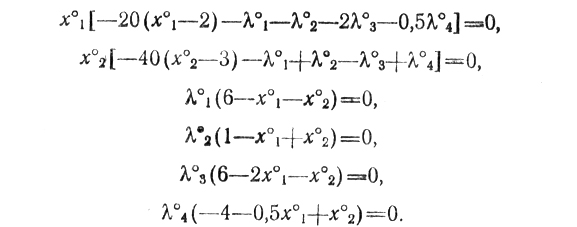
Среди возможных решений этой системы нужно выбрать теперь те, которые удовлетворяют соотношениям (2.9). Оказывается, этим свойством обладает одно решение: x^*₁ = 2, x^*₂ = 3, λ₁^* = λ^*₂ = λ₃^* = = λ^*₄ = 0; тот факт, что все λ_i^* - оказались равными нулю, a x^*_1,2>0, указывает на несущественность исходных ограничений задачи; проверка достаточных условий сводится к установлению факта выпуклости z (это можно сделать здесь простыми геометрическими построениями).

Теория Куна - Таккера позволяет заметно расширить круг задач нелинейного программирования, решение которых может быть получено в аналитическом виде.