3.2. Динамическое программирование и задачи с сепарабельной целевой функцией. Основное функциональное уравнение

Цель, преследуемая здесь, состоит в изучении особенностей метода динамического программирования и соответствующих вычислительных схем, приводящих к отысканию X^*, z^*. Этим оправданы упрощающие предположения, вводимые на разных этапах исследования в исходную общую задачу: найти

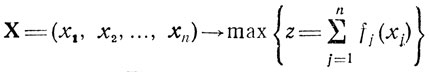
при g_i(X)≤b_i (i = 1,..., m), ∀x_j ≥ 0 (j = 1,..., n).

Предположим сначала, что в интересующей нас задаче присутствует только одно линейное ограничение, а сама она формулируется следующим образом: найти

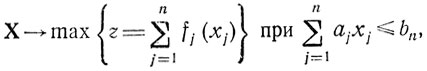
∀x_j≥0 - целые числа, ∀a_j>0 (j = 1,...,n).

Вид функций f_j(x_j) известен, искомый абсолютный максимум z обозначается как

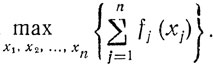
Пусть из совокупности x_j (j = 1,....,n) выбрана и зафиксирована величина х_n. Если в этой ситуации найти максимум z по остальным переменным х₁, х₂, ..., x_n-1, то окажется, что полученное решение будет зависеть от выбранного х_n. Действительно, вследствие сепарабельности z справедливо равенство

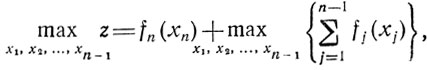
которое подтверждает предыдущее высказывание (слагаемое f_n можно вынести за знак max, поскольку оно связано только с х_n). При любом постоянном целом значении хп^0 переменные x₁, х₂, ..., х_n-1 должны ) удовлетворять неравенству

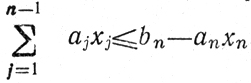
вытекающему из исходного ограничения, а также требованиям не отрицательности и целочисленности. Это влечет за собой зависимость от х_n и второго слагаемого выражения

max_{x1, x2,....,xn-1} z; таким образом вводится функция

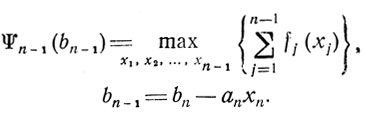
Если указанные операции проведены и Ψ_n-1(b_n-1) найдена, то можно утверждать, что искомая величина x^* = max_{x1, x2,....,xn} z есть

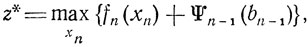(3.1)

где х_n может принимать значения 0, 1,..., [b_n/a_n] (равенство х_n = 1 + [b_n/a_n] недопустимо, так как приводит к нарушению ограничения

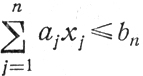
при ∀x_j≥0, ∀a_j>0).

Здесь важно заметить, что знание Ψ_n-1(b_n-1) сводит задачу поиска z^* к одномерной задаче оптимизации.

Имея в виду определение Ψ_n-1(b_n-1), потребуем найти

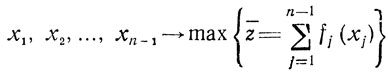
при

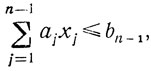
∀x_j ≥ 0 (целое), ∀a_j > 0 (j = 1,...,n - 1).

Очевидно, это требование полностью совпадает с исходной постановкой задачи (различие лишь в числе переменных x_j). Следовательно, отделив х_n-1 и повторив все предыдущие рассуждения, приходим к выводу:

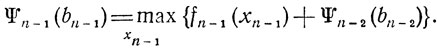(3.2)

По аналогии с первым случаем здесь х_n-1 может принимать значения 0, 1, ..., [b_n-1/a_n-1], а функция Ψ_n-2 определяется как

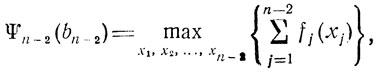
Если известна Ψ_n-2, можно найти Ψ_n-1, используя соотношение (3.2) и решая одномерную оптимизационную задачу подобно тому, как это делалось бы применительно к равенству (3.1). Ясно, что рассмотренный процесс может быть продолжен с целью выразить Ψ_n-2(b_n-2) через Ψ_n-3(b_n-3), Ψ_n-3 - через Ψ_n-4 и далее до тех пор, пока не будет найдена функция Ψ₁ (b₁) = max_x1 f₁ (x₁) при x₁ ∈ = {0, 1,...., [b₁/a₁], b₁ = b₂-a₂x₂. Таким образом, исходная задача с n переменными распадается на ряд однотипных задач с одной переменной, а процесс решения становится пошаговым.

Теперь можно дать следующие рекомендации по отысканию z^*:

- составляется последовательность функций

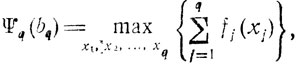
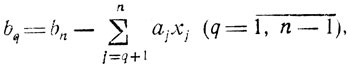
в которой Ψ₁ = max_x1 f₂(x₁) определяется непосредственно, а остальные функции - с помощью рекуррентного соотношения

-отыскивается z^* = max_{x1, x2,.....,xn} z в виде Ψ_n(b_n.

Соотношение

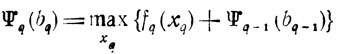(3.3)

представляет собой основное функциональное уравнение метода динамического программирования (уравнение Веллмана) в представленной здесь задаче с сепарабельной целевой функцией.