3.3. Частный алгоритм реализации метода. Представление и преобразование данных

Выше была изучена последовательность действий, приводящих к получению z^*, тогда как поставленная задача требует найти точку X^* = (x^*₁, х^*₂, ..., х^*_n), в которой z достигает значения z^*. Прежде чем перейти к описанию процедуры поиска X^*, заметим, что любая из величин b_q (q = 1,....., n-1) заключена в пределах 0≤b_q≤b_n, поскольку

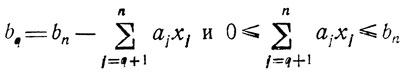
(из-за неотрицательности произведений a_jx_j). Для упрощения последующих рассуждений удобно предположить, что b_n и a_j (j = 1,..., n) - целые числа. Это условие вместе с условием "x_j - целые" (j = 1,....,n) определяет целочисленность всех b_q.

Порядок операций теперь может быть таким:

- выбирается переменная Х\, которой разрешается принимать целые значения от 0 до [b₁/a₁] при 0≤b₁≤b_n, пусть х̂₁ есть то значение х₁, при котором f₁(x₁) достигает максимума (ясно, что х̂₁ зависит от величины b₁); составляется таблица, где собраны все оптимальные x₁ = x̂₁, соответствующие допустимым b₁, причем каждому b₁ может отвечать несколько значений x̂₁ (табл. 3.1);

- определяются величины х̂₂(b₂), доставляющие максимум функции f₂(x₂)+Ψ₁(b₂-а₂х₂) при 0≤х₂≤[b₂/a₂], 0≤b₂≤b_n; результаты сводятся в табл. 3.2; при ее составлении удобно пользоваться результатами предыдущего шага, находя значения функции Ψ₁ для разных b₂-а₂х₂, которые в силу сделанных выше предположений положительны, целочисленны и не превышают b_n;

- рассмотренные операции повторяются для всех оставшихся x̂_q(b_q), (q = 3,..., n-1), и на каждом шаге используется предыдущая таблица, содержащая значения Ψ_q-1 в итоге возникает набор сходных по форме таблиц, содержащих перечни оптимальных x̂_q (q = 1,...., n - 1);

- анализируется последнее соотношение

вследствие того, что b_n задано однозначно исходными условиями задачи, таблица с х̂_n(b_n) состоит всего из одного столбца, который дополняет предшествующие результаты; теперь остается выбрать из множества найденных x̂_q (q = 1,...,n) одну или несколько совокупностей значений х^*₁, x^*₂, ..., х^*_n, определяющих X^*, z^*; сделать это можно с помощью уже составленных ранее таблиц;

- в качестве х^*_n принимается х̂_n (это необходимо, так как лишь при х_n = х̂_n достигается z^* независимо от того, каковы x̂_n-1,.....,x̂₁); если на предыдущем шаге получено несколько значений х̂_n, принимаемых здесь за х^*_n, последующий анализ проводится применительно к каждому из них, начиная с произвольно взятого;

- при известном х^*_n вычисляется b^*_n-1 = b_n-а_nх^*_n; теперь нужно обращать внимание лишь на тот столбец в таблице, содержащей сводку х̂_n-1 который соответствует именно b^*_n-1, потому что все другие величины b_n-1 допускались ранее в предположении 0≥b_n-1≤b_n, вытекающем, в свою очередь, из возможности принятия переменной х_n целого ряда неотрицательных значений; следовательно, х^*_n-1 = x̂_n-1 (b^*_n-1);

- при известных х^*_n и х^*_n-1 вычисляется b^*_n-2 = b_n - а_nх^*_n - а_n-1x^*_n-1, и по таблице, содержащей х_n-2, находим х^*_n-2 = x̂_n-2(b^*_n-2); тем же способом определяются остальные х^*_n-k (k = 3, n = 1); в результате получаем одну или несколько совокупностей величин x^*_j (конец процесса).

Таблица 3.1

Таблица 3.2

Обращаясь к терминологии предыдущего раздела, можно сказать, что в рассмотренной здесь процедуре поиска X^* содержанием шага (этапа) процесса принятия решений является определение очередного x^*_q (q = n,...., 1). Состояние процесса к началу этапа характеризуется соответствующей величиной b_q, и поэтому Ψ_q можно назвать функцией состояния.

В данном случае на каждом шаге встречался скалярный параметр b_q и требовалось найти лишь одну переменную x̂_q, хотя на практике чаще приходится иметь дело с векторами В_q и Х_q. В дальнейшем на это будет обращено внимание, но сейчас важнее оценить возможность отказа от введенного выше условия "x_j, a_j, b_n - целые числа", что позволит расширить круг задач, к которым применима приведенная здесь методология решения.

Исключив требование целочисленности x_j, a_j, b_n, можно приступить к решению задачи с сепарабельной целевой функцией

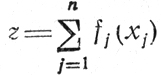
и ограничениями

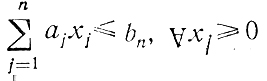
так же, как это было сделано выше, т. е. найти Ψ₁(61) = max_x1 f₁(х₁) при 0≤b₁≤b_n и далее все функции состояний

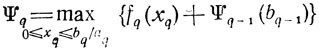
при 0≤b_q≤b_n, x_q≥0, q = 2,....,n, последняя из которых определит z^*. На этой стадии решения все различия сводятся к тому, что переменные x_q (q = 1,...., n-1) меняются в пределах от 0 до b_q/a_q (а не до [b_q/a_q]), и поиск частных максимумов по xq ведется, вообще говоря, иными методами. Например, в первом варианте задачи любая функция Ψ_q могла быть найдена перебором значений суммы f_q(x_q)-Ψ_q-1(b_q-1), а во втором варианте более перспективным может оказаться путь решения уравнений d/dx_q [f_q+Ψ_q-1] = 0.

При дальнейшем изучении различий между этими вариантами возникают вопросы о формах представления информации, которая ранее отражалась в табл. 3.1, 3.2, а также о способах определения оптимальных значений х^*_n-1, х^*_n-2, .. при известных x̂_q(b_q) (q = 1,....,n). Оба вопроса не являются принципиальными, хотя и важны сами по себе. Первый решается применительно к конкретной обстановке (x_q и Ψ_q могут быть представлены, в частности, в виде формул или графиков, если их исследованием занимается человек, в виде систем уравнений или сеток значений, если все "передано" вычислительной машине и т. д.). Это, в свою очередь, накладывает отпечаток на способы получения x^*_j (j = n,....,1), среди которых наиболее надежными можно считать непосредственные вычисления значений Ь^*_n-1 ,..., b^*₁ и x^*_n-1 = x̂_n-1(b^*_n-1), x^*_n-2 = x̂_n-2 (b^*_n-2),....

Таким образом, отбрасывая требования целочисленности x_j, a_j, b_n, мы не меняем метод решения в целом, меняются лишь приемы промежуточных вычислений.