3.4. Векторный параметр состояния. Проблема большой размерности

Серьезные трудности возникают при появлении векторного параметра состояния В_q. Условия, в которых это

происходит, иллюстрирует следующая задача: найти

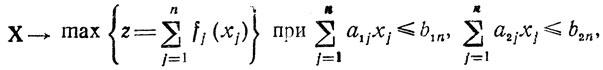
∀x_j≥0-целые числа (случай m = 2).

Полагая, как и ранее, все a_1j, a_2j, b_1n, b_2n положительными и целыми, заметим, что любая функция из последовательности Ψ_q (q = 1,...,n) является теперь функцией

двух аргументов b_1q и b_2q, где

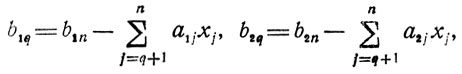
поскольку все х_q, по которым ищутся максимумы вида max{f_q(x_q)+_q-1}, должны удовлетворять требованиям

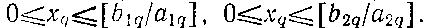
Это возможно тогда, когда неотрицательная величина х_q не превышает меньшего из значений [b_iq/a_iq] (i = 1, 2), т. е. 0≤x_q≤min{[b_1q/a_1q], [b_2q/a_2q]}. Следовательно, приступая

к определению

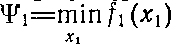
необходимо предварительно найти

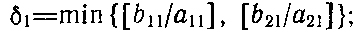
затем, повторяя на каждом шаге аналогичные операции, нетрудно составить

последовательность функций

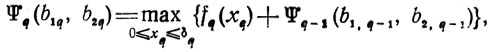
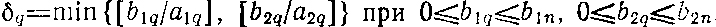
Вместе с Ψ_q определяется и x̂_q(b_1q, b_2q); для q = n имеем

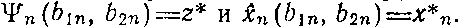
Если свести всю информацию Ψ_q и x̂_q в таблицы, то для каждого номера q придется включить b_1nb_2n значений δ_q и такое же количество значений Ψ_q, x̂_q, найденных в результате решения задач об отыскании максимумов сумм f_q+Ψ_q-1; после этого q-я таблица примет вид (табл. 3.3)

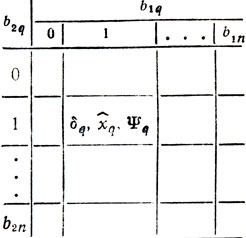
Таблица 3.3

Ясно, что не только заполнить, но и использовать такие таблицы для получения оптимальных x^*_n-k = x̂_n-k (b^*_{1, n-k}, b^*_{2, n-k}) чрезвычайно трудно (особенно когда b_1n и b_2n достигают десятков и сотен единиц) . В этом - главное препятствие на пути использования метода динамического программирования в задачах с векторным параметром B_q. Даже небольшое число составляющих В_q (порядка 3-4) может привести к неразрешимости задачи из-за чрезмерных требований к объемам памяти и быстродействию вычислительных машин. В основе этого утверждения лежит очевидная оценка

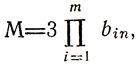
связывающая количество М чисел δ_q, х̂_q, Ψ_q подлежащих запоминанию, с величинами b_in, входящими в ограничения

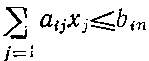
(i = 1,....,m). Если m = 2, b_1n = b_2n = 10, то M=300 (объем таблицы типа 3.3), но при m = 4, b_in = 100 (i = 1, 4) получаем М = 3 × 10⁸. К тому же с ростом числа составляющих В_q усложняются процедуры поиска δ_q и особенно x̂_q, что вызывает дополнительные затраты средств и времени на реализацию метода.

Обратимся теперь к случаю, когда на каждом шаге решения приходится иметь дело с вектором X_q. Соответствующая постановка задачи может иметь вид: найти

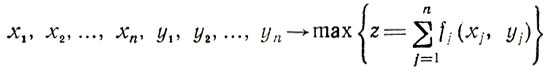
при

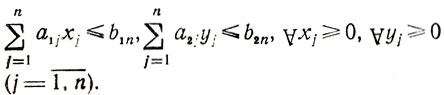
целые числа.

Сохраняя все предыдущие рассуждения, нетрудно показать, что основное функциональное уравнение записывается в рассматриваемом случае как

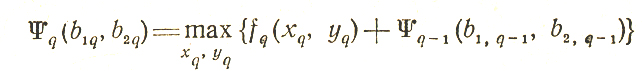
(для этого достаточно зафиксировать сначала величины х_n, y_n, затем представить x^* в виде

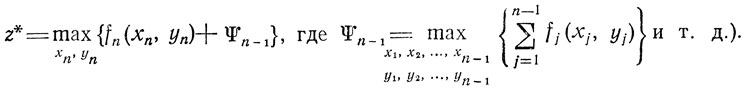
Таким образом, особенностью здесь является усложнение исследований, проводимых в рамках очередного этапа с целью указать X̂_q = (x̂_q, ŷ_q) (решается многомерная оптимизационная задача).

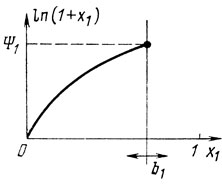
Рис. 3.2

Дальнейшие изменения условий исходной задачи и приближение их к общим условиям, сформулированным на с. 72, должны привести к новым способам отыскания ними X^*, z^*, однако уже сейчас можно сделать выводы, касающиеся применения метода динамического программирования в

задачах с сепарабельной целевой функцией. В первую очередь необходимо констатировать неизменность основного функционального уравнения, вид которого определяется видом z. Различные

вариации ограничивающих условий приводят лишь к изменению деталей этого соотношения, не затрагивая его структуры в целом (анализ функциональных уравнений другого типа станет необходимым при переходе к какому-либо новому классу задач). Линейные ограничения-неравенства,

рассмотренные выше, были выбраны из соображений простоты и наглядности оценок, характеризующих основные этапы решения (прежде всего упростилось определение пределов, в которых изменяются значения x_q и b_q (q = 1,...., n-1)). В более сложных случаях могут возникнуть трудности поиска и описания параметров b_q, функций Ψ_q, решений x̂_q. Ниже даны иллюстративные примеры.

Пример: найти x₁, х₂, х₃ → max {z = ln (1 + х₁) + х₂ + х²₃} при x₁ + x₂ + x₃ ≤ 1, ∀x_j ≥0 (j = 1,...., 3), x₃-целое число (здесь b_n ≡ b₃ = 1).

Решение: ищем первую функцию состояния Ψ₁ = max {ln(1+x₁)} при 0≤b₂≤1, 0≤b₁≤1, где b₁ = 1-x₃-x₂; для этого достаточно построить график (рис. 3.2), дающий x̂₁ = b₁ и Ψ₁ = ln (1+x̂₁) = ln (1+b₁);

функция ₂ определяется как Ψ₂ = max {x₂+Ψ₁} при 0≤b₂≤1, 0≤b₂≤1, где b₂ = 1-x₃; пользуясь соотношением b₁ = b₂-х₂, получаем Ψ₁ = ln(1+b₂-x₂) и, следовательно,

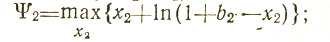
производная

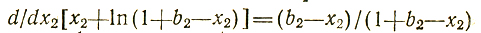
обращается в нуль при х₂=b₂, поэтому (после проверки достаточных условий экстремума) принимаем х̂₂ = b₂ и Ψ₂ = x̂₂+ln (1+b₂-х₂) = b₂;

функция

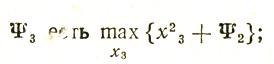
учитывая равенство b₂ = 1 - х₃, имеем

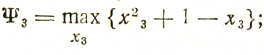
переменная х₃ целочисленно и в условиях рассматриваемой задачи может принимать лишь значения 0, 1; независимо от этого x²₃+1-x₃=1 следовательно, x̂_3(I) = 0 и x̂_3(II) = 1;

теперь остается выбрать из имеющихся x̂_j (j = 1,....,3) те значения,, которые будут приняты в качестве x^*_j; положив x^*_3(I) = 0 и x^*_3(II) = 1, получаем b^*_2(I) = 1-x^*_3(I) = 1 и x^*_2(II) = 0, что дает x^*_2(I) = x^*_2(II) = 0; далее, b^*_1(I) = 1-x^*_3(I)-x^*_2(I) = 0, b^*_1(II) = 0, т. е. x^*_1(I) = x^*_1(II) = 0;

таким образом, найдены оптимальные решения: x^*₁ = 0, x^*₂ = 1, x^*₃ = 0, z^* = 1 и x^*₁ = 0, x^*₂ = 0, x^*₃ = 1, z^* = l.

Пример: найти

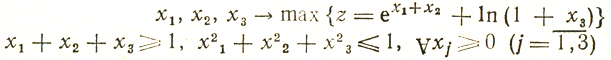
(здесь нужно планировать двухэтапный процесс решения, исследуя на первом этапе задачу с векторным аргументом).

Решение: первая функция состояния представляется в данном случае как

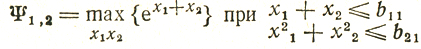
где

b₁₁ = 1 - x₃, b²₂₁ = 1 - х²₃ и 0≤b₁₁≤1, 0≤b²₂₁≤1; поскольку величина х₃ не превышает 1, имеем b₁₁≤b²₂₁ (знак равенства появляется лишь при x₃ = 0 или x₃ = 1); следовательно, достаточно рассматривать область допустимых x₁, х₂, показанную на рис. 3.3;

величина e^x₁+x₂ тем больше, чем больше сумма с = х₁ + х₂; увеличение с (от значения b₁₁) возможно до тех пор, пока система

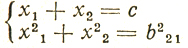
имеет решения; предельным в этом смысле является с = b₂₁√2 (рис. 3 3), поэтому х̂₁ = х̂₂ = b₂₁√2/2 и Ψ_1,2 = e^b₂₁√2;

функция Ψ₃ ищется в виде

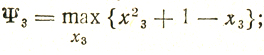
качественный анализ изменения величин в фигурных скобках показывает, что искомый максимум достигается при х̂₃ = 0 и составляет e^√2≈4,1;

положив х^*₃ = х̂₃ = 0, находим b²₂₁ = 1, т. е. х^*₁ = х^*₂ = √2/2; решение задачи в целом есть x^*₁ = √2/2, х^*₂ = √2/2, х^*₃ = 0, z^* = 4,1.

Исследование задач с сепарабельной целевой функцией позволило более наглядно представить вычислительные аспекты метода динамического программирования, которые приобрели большое значение в связи с возможностями использования быстродействующих ЭВМ. Вместе с тем функциональные уравнения, отражающие принцип оптимальности, оказываются в отдельных случаях разрешимыми аналитически, что позволяет избежать числовых расчетов и связанных с ними затрат времени.

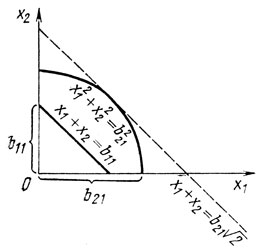
Рис. 3.3