4.3. Методы возможных направлений. Условия выбора вычислительной схемы

Идея методов возможных направлений проста: из начальной допустимой (по условиям задачи) точки Х₀ осуществляется переход к новой допустимой точке, в которой значение целевой функции 2 лучше, чем в Х₀; этот процесс продолжается до тех пор, пока сохраняется возможность улучшения z.

Каждый шаг решения основан здесь на двух операциях-выборе подходящего направления, двигаясь в котором можно достичь лучших z (пусть на достаточно малом перемещении), не выходя за пределы области U, и оценке требуемой величины перемещения. По такой схеме работает большое количество численных методов, причем результатом обычно является указание точки Х_∞, подозрительной на экстремум. Если определена очередная точка Х_k, то переход к следующей точке осуществляется в соответствии с формулой

где a_k - величина k-го шага; r_k - единичный вектор, в направлении которого производится этот шаг. Интерпретации названных условий даны ниже; для простоты сначала предполагается отсутствие ограничений на выбор X (т. е. U≡R_n).

Метод наискорейшего спуска

В основе метода наискорейшего спуска лежат следующие утверждения:

-в качестве r_k всегда выбирается вектор градиента

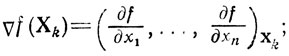
-величина а_k определяется либо условием

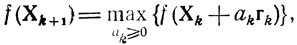
либо

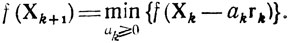
Преимущества такой схемы поиска X^* заключаются в возможности получать максимальные приращения |z| при переходах от одной точки X к другой (см. также гл. 6). Рассматриваемый метод является одним из наиболее рапространенных численных методов; в его названии отражена идея скорейшего достижения точки минимума z.

Для доказательства сходимости введем следующие предположения:

1) рассматривается задача на отыскание безусловного минимума f(X), причем множество {X^*} не пусто;

2) f(X) является выпуклой вниз и дифференцируемой функцией, т. е. (∇f(X₁), X₁-X₂)≥f(X₁)-f(X₂) при Х₁≠Х₂, Х₁, Х₂∈R_n; в частности, (∇f(X_k), X_k-X^*)≥f(X_k)-f(X^*) > 0;

3) множество {X} точек X, обладающих свойством f(X)≤f(X₁), ограничено, т. е. diam{X} = D<∞ (здесь Х₁ - начальная точка поиска);

4) для любых X_k, X_l отличных от X^*, выполнено условие

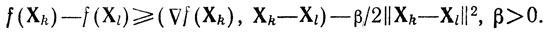
Использование этих замечаний позволяет получить оценку изменения разностей f(X_k)-f(X^*),k = 1,2,..., и тем самым дать ответ на традиционный вопрос о скорости сходимости процесса поиска X^*, что является косвенным подтверждением замкнутости W(X_k).

Из очевидного равенства

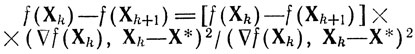
и замечания 2) следует

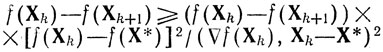
или

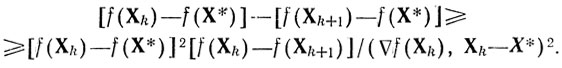
Если f(Х_k)-f(X_k+1)>0 (подобное требование является общим для поисковых методов, см. теорему 11), то приведенное выше неравенство легко представить в виде t_k-t_k+1≥b_kt²_k, b_k>0, t_k>t_k+1 его решением служит

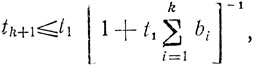
k≥1 (чтобы убедиться в этом, достаточно записать рассматриваемое неравенство как t_i/t_i+1-1≥b_it²_i/t_i+1 или l/t_i+1-1/t_i≥b_it_i/t_i≥b_i и провести суммирование по номерам t). Таким образом,

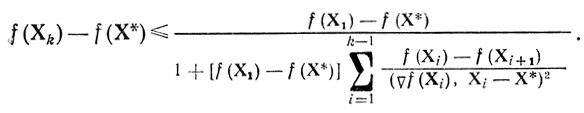(4.3)

Теперь проблема оценки разностей f(X_k)-f(X^*) сводится к анализу свойств слагаемых, собранных под знаком суммы в знаменателе (4.3). Для исследуемого случая

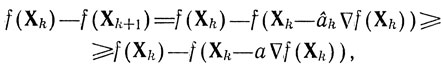
где â_k - величина шага, найденная в результате минимизации f(X_k-a_kr_k) (см. замечание 1)); а - произвольное неотрицательное значение параметра а_k. Согласно условию 4) имеем a∇f(X_k) - f(X_k-a∇f(X_k))≥(∇f(X_k), a∇f (Х_k)) - β/2||a∇/(X_k) ||² = a|| ∇f(X_k) ||²-a²β/2|| - a²β/2||∇f(X_k) ||². Положив в последнем неравенстве а = 1/р, получаем f(X_k)- f(X_k+1)≥||∇f(X_k) ||²/2β. Далее, согласно неравенству Коши - Буняковского

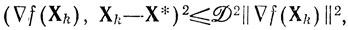
поэтому

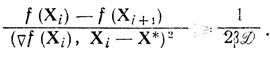
Замена каждого слагаемого суммы

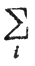
в (4.3) на 1/2βD² только усилит отношение (4.3), следовательно,

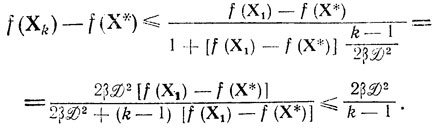(4.4)

Нетрудно видеть, что f(Х_k)→f(Х^*) при k→∞, т. е. имеет место сходимость (в данном случае - слабая) метода наискорейшего спуска.

Решающую роль в получении оценки (4.4) играли предположения 1)-4). Далеко не всегда исследователь имеет в своем распоряжении столь обширные сведения

6 особенностях функции f(X), и проблема обеспечения сходимости остается одной из центральных проблем разработки эффективных методов поиска оптимума.

Обобщенный метод Ньютона

Активное использование только первых производных df/dx_j в ходе определения Х_k+1, k = 1, 2, ..., может оказаться недостаточным в заключительной фазе поиска X^*, z^* из-за необходимости более точной аппроксимации f(X). Это приводит к идее учета производных высших порядков (прежде всего - второго порядка) для улучшения показателей вычислительного процесса (например, скорости сходимости вблизи X^*).

Обобщенный метод Ньютона базируется на представлении f(Х_k+1) в виде

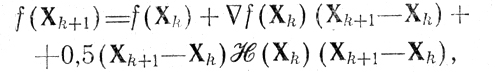
где H(X_k)-матрица вторых частных производных функции f(X) в точке Х_k (гессиан). Из необходимого условия эстремума ∇f(X^*) = 0 следует ∇f(Х_k) + H(Х_k) (Х^*-Х_k) = 0, поэтому (при обратимой матрице H) имеем (X^*-Х_k) = -H^-1 (Х_k) ∇f(Х_k). Направление -H^-1(Х_k) ∇f(X_k) используется при организации переходов; величина ад определяется уже встречавшимся требованием

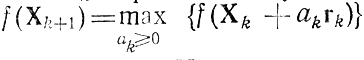
Сходимость метода Ньютона доказывается в тех же предположениях относительно свойств f(X), которые были сделаны при описании метода наискорейшего спуска; необходимые коррективы связаны с существованием и обратимостью H(Х_k).

Многократные вычисления производных функции f(X), сопровождаемые обращениями гессиана, оказываются (в общем случае) весьма трудоемкими, поэтому желательно иметь и такие методы, которые были бы ориентированы на оценки значений самой f(X).

Метод циклического координатного спуска

Пусть заданы n единичных векторов е₁ ,..., е_n, направления которых совпадают с положительными направлениями соответствующих координатных осей. Предлагается оптимизировать f(X) поочередно по каждому из указанных направлений; после того как завершится исследование направления е_n, происходит возврат к e₁ и процесс (цикл) повторяется. Если X_k - очередная точка, куда совершен переход, a e_j - вектор, определяющий направление дальнейшего "движения" (1≤j≤n), то Х_k+1 находится из условия

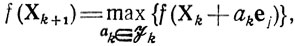
Х_k+2 - из условия

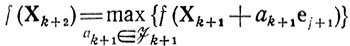
т.д. (случай max z); здесь k-множество допустимых а_k.

Сходимость метода обеспечивается в предположениях, что f(X) имеет непрерывные первые производные df/dx_j (j = 1,....,n) и для любого X_k на направлении произвольно взятого е_j (1≤j≤n) существует единственное значение a_k=â_k, доставляющее максимум f (X_k + a_ke_j).

Очевидно, можно разрабатывать и другие алгоритмы поиска оптимума, объединяемые идеей выбора допустимых направлений r_k. В частности, стремление учесть не только необходимые, но и достаточные условия экстремума приводит к так называемым методам второго порядка (здесь определяющими являются особенности матрицы H); стремление объединить полезные свойства разных методов реализуется в методе сопряженных градиентов и т. д. Важно заметить, что разнообразие подходов к проблеме выбора возможного направления перемещений от X_k к X_k+1 не затрагивает принципа получения Х_k+1 при известном r_k (оптимизация по пара-

метру а_k). Следовательно, алгоритмическое отображение W(X_k) характеризующее рассматриваемую группу методов, всегда представимо как W(X_k) = W_IW_II, где W_I - отображение, определяющее рациональное а_k = â_k, W_II - отображение, определяющее нужное направление r_k.

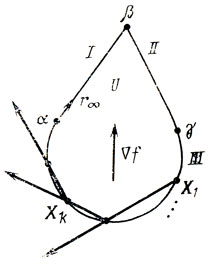
Рис. 4.1

Сравнительная простота условий сходимости алгоритмов, основанных на использовании формулы (4.2), объясняется двумя причинами - наличием удобных свойств функции f(X) (гладкость, единственность â_k и т. п.) и отсутствием ограничений на выбор Х_k. Это затрудняет практическое применение методов возможных направлений в том виде, как они были даны выше; возникает необходимость дополнительных исследований с целью внести коррективы, учитывающие ограниченность области U.

Главным осложнением, связанным с требованием учета границ U, является возможная не замкнутость отображения W_I; следствием этого бывает нарушение сходимости метода (так называемое заклинивание). Оно выражается в том, что применяемый алгоритм начинает вырабатывать последовательность {Х_k}, сходящуюся к Х_∞≠Х^*. Пример подобного отклонения дан на рис. 4.1, где изображена область U, границами которой служат прямые I, II и сопряженная с ними дуга окружности III. Если принять одну из точек окружности за начальную точку X₁ и на каждом шаге использовать (в качестве заданного) направление хорды, соединяющей X_k с серединой дуги (α, Х_k), то можно ожидать возникновения последовательности {Х_k}, сходящейся к Х_∞ = α (для этого достаточно, чтобы вектор ∇f был постоянно направлен так, как показано на рис. 4.1); очевидно, направление тк перейдет в пределе (при k→∞) в r_∞ = (αβ). Рассматривая теперь последовательность {X_k+1}, k = 1, 2, ..., приходим к заключению: в принятых предположениях ее предельная точка X_∞+1 совпадает с Х_∞ = α, хотя правило переходов требует (а свойства ∇f допускают) выбрать X_∞+1 = β; следовательно, X_∞∉W_I(X_∞, r_∞), отображение W_I незамкнуто в Х_∞, и Х_∞≠Х^*.

Полезно обратить внимание и на следующее обстоятельство: как и ранее, W_I при имеющихся Х_k, r_k указывает точку Х_k+1 доставляющую экстремум (для определенности-максимум) функции f(X) на прямой, выходящей из X_k в направлении r_k, однако в задаче с ограничениями дополнительно требуется, чтобы отрезок, соединяющий X_k с X_k+1, целиком принадлежал U (это особенно важно учитывать тогда, когда область U невыпукла). Таким образом, проблема анализа сходимости заметно усложняется. В ряде случаев ее успешному решению способствует использование результатов теоремы сходимости (13), приводимой здесь без доказательства: если при поиске экстремума непрерывно дифференцируемой целевой функции f(X) метод возможных направлений дает последовательность {X_k}, k = 1, 2, содержащую подпоследовательности, которые имеют предельными X, r значения Х_∞, r_∞, допускают выполнение неравенства (∇f(X_∞), r_∞)>0 и обеспечивают принадлежность всех Х_u + а_ur_u области U при любом а_u ∈ [0, δ], δ>0, то пределом любой сходящейся подпоследовательности будет точка X^*.

Рассматриваемые условия не только обеспечивают улучшение z при перемещениях вдоль r_k, но и учитывают возможное появление препятствий в виде границ области U. Вводится регулирование длины шага (параметр δ) на случай, когда какая-то из точек X_k окажется вблизи границы; все указанные особенности должны сохраняться и при предельном переходе (k→∞).

На практике опасность неудачного выбора r_k может быть устранена запоминанием точек и участков границы. к которым приводит используемая вычислительная процедура, а также внесением других аналогичных корректив в логическую схему алгоритма поиска X^*, z^*. Это часто вызывает существенные изменения в подходах к решению задачи.

Метод ε-возмущений

Обратимся к задаче математического программирования: найти Х→max{z = f(Х)} при φ_i(Х)≥0, i = 1,...., m. Считая f (X) и все φ_i(Х) непрерывно дифференцируемыми, определим в некоторой допустимой точке X_k множество J_ε номеров i, для которых φ_i(Х^*)≤ε (здесь ε - неотрицательное число, указывающее степень близости Х_k к границе фφ_i = 0, i∈J; при ε = 0 точка X_k попадает на рассматриваемую границу; с увеличением ε состав множества J_ε расширяется). Если теперь выбирать с учетом условий φ_i(X_k)≤ε(i∈J_ε), то опасность выхода на соответствующие границы исключается или отдаляется настолько, что ею можно пренебречь. Подобные соображения лежат в основе метода ε-возмущений.

Пусть X_k и ε с заданы; пусть далее σ-параметр, имеющий смысл производной по направлению. Ставится цель найти направление r_k=r^*_k, доставляющее шах а при (∇f(X_k), r_k)-σ≥0, (∇φ_i(X_k), r_k)-σ≥0 (i∈J_ε), σ≥0 (увеличение а означает, с одной стороны, попытку сблизить положения r_k и ∇f, а с другой стороны, отдалиться от границ φ_i = 0, i∈J_ε; достижимый компромисс характеризуется здесь получаемым значением max σ = = σ^*, зависящим от Х_k, ε). Если окажется σ^*(Х_k, ε)>0, то рекомендованное выше правило выбора r_k = r^*_k обеспечит выполнение неравенств (∇f(X_k), r_k) > 0, (Δφ_i(Х_k), r_k) >0, (i∈J_ε) и шаг (пусть небольшой) в направлении r^*_k позволит улучшить 2 с одновременным сохранением допустимости X_k+1. Другим важным моментом является то, что при ε = 0 и σ^* (Х_k, 0) = 0 в точке Х_k выполняются условия Куна - Таккера.

Алгоритм метода ε-возмущений представляется теперь в следующем виде:

а) выбирается допустимая начальная точка X₁ и принимается ε₁>0;

б) решается вспомогательная задача определения r^*₁, σ^*(Х₁, ε₁);

в) вычисляется Х₂ согласно требованию Х₂∈W_I(X₁, r^*₁);

г) принимается ε₂≤ε₁ и процедуры б), в) повторяются сначала для Х₂, ε₂, а затем для остальных X_k, ε_k(k = 3, 4, ...);

д) поиск экстремума завершается, если очередная точка Хи удовлетворяет условиям Куна - Таккера.

Доказательство сходимости (при k→∞) рассмотренного алгоритма основывается в значительной степени на оценках поведения последовательности ε_k (это нужно для выполнения условий теоремы (13)).

Использование методов возможных направлений не исчерпывает всей проблемы организации поиска X^*, z^*. Практически трудности соблюдения ряда условий, от которых зависит сходимость конкретного метода, делают необходимой разработку иных подходов к указанной проблеме.