4.4. Методы штрафных функций. Формы учета ограничений задачи

Рассматриваемые методы основаны на идее преобразования оптимизационной задачи с ограничениями в последовательность задач без ограничений. С этой точки зрения первым представителем изучаемой группы методов является классический метод множителей Лагранжа (см. гл. 2), позволяющий исследовать безусловный экстремум Φ(Х, Λ) с целью отыскания условного экстремума f(X).

Пусть дана следующая задача математического программирования: найти Х→min{z = f(Х)} при φ_i(Х)≥0 (i = 1,...,m); ее областью определения, как обычно, является U⊂R_n. Если положить, например, F(Х) = 0 при X∈U, F(X) = ∞ при X∉U и составить функцию L(X) = f(X) + F(Х), то решение новой задачи об отыскании точки X∈R_n, доставляющей min L(X), будет обладать свойствами X∈U, min L(X) = L(X̂) = f(X̂) и, следовательно, Х̂ ≡ Х^*.

Функция F(Х), налагающая бесконечно большой штраф за выход X из U, называется штрафной функцией.

Непосредственное использование F (X) в том виде, как она дана выше, затруднено тем, что приходится оперировать с бесконечно большими величинами, поэтому на практике стремятся аппроксимировать F(X) последовательностью функций F_k(X), приближающейся в пределе (при k→∞) к F(Х).

Существуют две разновидности методов штрафных функций - методы внутренней и внешней точки. В первом случае введение F(Х) препятствует выходу точек последовательности {Х_k} из U и нарушению условия

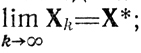
во втором случае присутствие F(Х) должно предотвратить блуждание точек X_k далеко за пределами U при сохранении требований

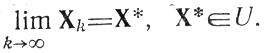
Особенности организации поиска X^*, z^* здесь удобно исследовать применительно к приведенной выше задаче минимизации f(X).

Метод внутренней точки

Обозначим множество всех внутренних точек области U как U₀ и зададим f(Х) следующими условиями: - F(Х) непрерывна и принимает положительные значения при Х∈U₀;

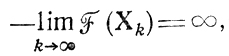
если {X_k} - произвольная бесконечная последовательность точек в U₀, сходящаяся к Х_Γ, причем φ_i(Х_Γ) = 0 хотя бы для одного номера i.

Пусть S(r) - скалярная функция аргумента r, обладающая свойствами: S(r₁) > S(r²) >0 при r₁>r₂>0;

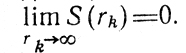
Произведения вида S(r_k)F(Х) могут рассматриваться в качестве "рабочих" значений штрафной функции.

Алгоритм метода внутренней точки включает в себя:

а) выбор начальных X₁∈U₀, r₁>0 и составление функции L (X, r₁) = f(X) + S(r₁)F(X);

б) решение задачи об отыскании точки X̂ локального безусловного минимума L(X, r₁) и принятие ее за X₂ (выше отмечалось, что такая X̂ обязательно будет принадлежать U₀, иначе она перестанет быть точкой минимума L);

в) выбор нового положительного значения r = r₂<r₁ и новой функции L(X, r₂) = f(Х) + S(r₂)F(Х); определение точки X̂ для L(X, r₂) и переход в нее (Х₃);

г) повторение процедуры в) для Х₃, Х₄, ... при r₃<r₂, r₄<r₃, r₅<r₄, ... до достижения (с заданной точностью) решения исходной задачи.

Иногда бывает трудно найти X₁∈U₀ (число ограничений велико и проверять произвольно взятую X₁ нецелесообразно или X₁ задана сразу как граничная точка и т. п.). В этой ситуации можно применить метод внутренней точки и для поиска приемлемой в указанном смысле X₁. Пусть X̄₁ удовлетворяет условиям φ_i(Х)>0 (i∈J⁺), φ_i(Х)≤0 (i∈J^-), и нужно построить такую последовательность {Х̄_1k}, чтобы величина

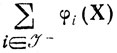
возрастала, но ни одно из ограничений φ_i(Х)>0(i∈J⁺) не нарушалось. Очевидно, желаемого результата можно достичь, минимизируя функцию

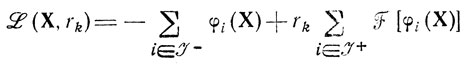
при строго убывающих положительных r_k. Здесь по мере перехода от одной точки X̂ к другой элементы множества J^- переходят в J⁺ признаком окончания процесса является J^- = ∅.

Метод внешней точки

Предположим, что функция (X) обладает теперь следующими свойствами: она непрерывна и строго положительна везде в Rn, кроме точек Хе?/; в них она равна нулю. Функция S(r) вводится в таком виде: S(r₂)>S(r₁)>0 при r₂>r₁>0,

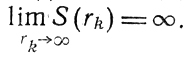
Алгоритм метода внешней точки включает:

а) выбор начальных r₁>0, X₁∈C и составление функции L(X, r₁) = f(X) + S(r₁)F(X) (здесь G - произвольное компактное множество, содержащееся в R_n, причем U⊂G);

б) решение задачи об отыскании точки X̂ локального безусловного минимума L (X, r₁) и принятие ее за Х₂;

в) выбор нового r = r₂>r₁ и новой L(X, r₂) = f(Х) + S(r₂)F(Х); определение течки X̂ для L(X, r₂) и переход в нее (Х₃);

г) повторение процедуры в) при строго возрастающих r_k→∞; можно показать, что при r_k→∞ последовательность точек X̂ стремится к X^* (удаление X_k от U с ростом k привело бы к увеличению штрафа, поскольку r_k→∞ и для Х∉U).

Практическое применение рассматриваемых методов может быть осложнено присутствием ограничений-равенств φ_i(Х) = 0, определенностью f(X) не во всех точках X∈R_n и т. п. Это вызывает необходимость формирования комбинированных алгоритмов, к которым обычно предъявляется требование гарантировать соблюдение одних ограничений на протяжении всего вычислительного процесса, а других - только при приближении к оптимуму. Такой подход расширяет круг задач, решаемых предложенным способом.

При исследовании сходимости методов штрафных функций удобно представить соответствующие алгоритмы общим отношением X_k+1∈W_k(X_k). Это облегчает использование следующей теоремы (14):

если для некоторых k множество W_k(X_k) пусто, то алгоритм указывает, что или X_k = X^*, или U=∅;

если алгоритм вырабатывает бесконечную последовательность точек X_k и ни одна из них не является решением задачи,то в R_n должно существовать компактное подмножество, которому принадлежат все X_k, а непрерывная функция z = f(X) удовлетворяет на этих X_k условиям: a) f(X_l)≥f(X_k) для всех l≥k+v_k (здесь v_k-некоторое число, относящееся к данному X_k), б) для любой подпоследовательности {X_k}, сходящейся к Х'≠Х^*, либо существует такое k=k', что f(X_k')<f(Х'),либо существует сходящаяся подпоследовательность {f(Х_k')},имеющая своим пределом f(X̂)<f(X').

Опуская доказательство, заметим, что сформулированные положения относятся к задаче минимизации f(X) на множестве U; вместо строгого улучшения f(X) на каждом шаге требуется улучшение лишь после v_k шагов; вместо замкнутости алгоритмического отображения W_k(X_k) требуется выполнение условий а), б).

Сходимость того или иного метода (из рассмотренных в этом разделе) сравнительно легко устанавливается в случаях, когда f(X) и φ_i(Х) (i = 1,..., m) непрерывны, а множество U - компактно; может также понадобиться, чтобы X₁∈U₀ и в любой окрестности X^* существовали точки Х∈U₀ (т. е. X^* не была бы изолированной от указанных X). Ниже даны примеры использования штрафных функций.

Пример: найти х₁,х₂→min {z-x₁+x₂} при x₁≥0, -x²₁+x₂≥0.

Решение: ориентируясь на применение метода внутренней точки, введем в рассмотрение функции

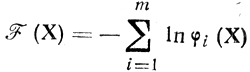
S (r) = r; тогда L (X, r) = х₁ + х₂ - r[ln (- х²₁ + х₂) + ln х₁]; существование точек X̂ для произвольных r связано с равенствами

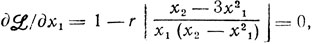
(достаточные условия min L здесь выполняются); следовательно,

всегда точки X будут принадлежать кривой х₂=х₁+3х²₁, которая целиком лежит внутри области -x²₁+x₂≥0, х₁≥0 (исключение

составляет только Х̂ = (0, 0)); каждую такую X можно принять за X₁ (условие X₁∈U₀ выполнено); далее следуют обычные операции:

а) принимается X₁ = (1,4) и r₁ = 1; L (X, r₁)=x₁+x₂-ln [х₁(х₂-х²₁)];

б) решается система dL(Х, r₁)/dx₁=0, dL(Х, r₁)/dx₂= 0, что дает Х̂ = (0,5; 1,25) = Х₂;

в) принимается r₂ = 0,5; L(Х, r₂)=x₁+x₂-0,5ln [x₁(x₂-x²₁)]; точкой минимума L здесь является Х̂ = (0,31; 0,59) = Х₃;

г) процедура отыскания X̂ повторяется для r₃ = 0,25 r₄ = 0,1,...; это позволяет получить Х₄ = (0,18; 0,28) и т. д.; нетрудно видеть, что последовательность {Х^*} стремится к X_∞ = (0, 0), которая становится подозрительной на экстремум;

д) в тех точках окрестности Х_∞, которые принадлежат U, функция f(X) = x₁+x₂ положительно определена (достаточное условие минимума), поэтому Х^* = (0, 0) и z^* = 0.

Выбор другой последовательности {r} привел бы лишь к появлению новой последовательности {Х_k}; конечный результат решения задачи сохраняется.

Пример: найти х₁, х₂→min{z = -х₁х₂} при х₁+х₂≥0, 1- х₁ + х²₂ ≥ 0.

Решение: ориентируясь на применение метода внешней точки положим

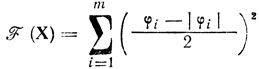
и S(r) = r; учитывая, что

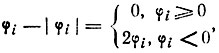
получим

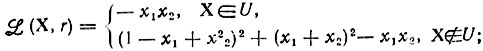
поиск точек X̂ здесь несколько усложняется (производные dL/dх_j разрывны), но допускается практически произвольный выбор Х₁; в остальном вычислительная схема сходна с той, что рассмотрена в предыдущем примере, поэтому можно взять X₁ = (1,1), r₁ = 1 и построить последовательность {(0,89; 0,64), (0,77; 0,62), (0,73; 0,61); (0,67; 0,58)...} для r, равных соответственно 1, 2, 3, 10,...; предельной точкой здесь является Х_∞ = (2/3, 3/3); проверка достаточных условий минимума f(X) подтверждает ее оптимальность, т. е. Х^* = (2/3, √3/3), z^* = 2 √3/9.