4.5. Методы отсечений. Искусственная линеаризация задачи

Методы отсечений имеют своей целью свести исходную нелинейную задачу математического программирования к более простой ее разновидности (например, к задаче линейного программирования). Это делается путем последовательной замены имеющейся области U рядом несложных по своей конфигурации областей. Существующие варианты методов отсечений характеризуются принятыми способами аппроксимации границ U, предполагаемыми свойствами функций f(X), φ_i(Х), i = 1,....,m и т. п.

Метод аппроксимации границ области

Пусть дана следующая нелинейная задача: найти Х→max {z = f (X)} при φ_i(Х)≥0 (i = 1,...,m). Вводя в рассмотрение скалярную величину 0, можно дать другую интерпретацию этих условий: найти X, ω→max ω при f(X)-ω≥0, φ_i(Х)≥0 (i = 1,....,m). Таким образом, добавлением одной переменной и одного ограничения можно заменить задачу с целевой функцией общего вида задачей с линейной целевой функцией.

Пусть теперь φ(Х, ω) = min{f(X)} - ω, φ₁(Х),... ..., ф_m(Х)}. Требование φ(Х, ω)≥0 равносильно совокупности перечисленных ограничений, поэтому новая интерпретация исходных условий находит свое выражение в задаче: найти X, ω→max ω при φ(Х, ω) ≥ 0. Здесь область U_ω допустимых X, ω определяется единственным неравенством φ>0, и легко предположить, что какая-то из внутренних точек (Х₁, ω₁) этой области известна (по крайней мере, ее можно найти методом штрафных функций, см. § 4.4). Формально параметр со может рассматриваться как (n+1)-я составляющая вектора Х = (x₁, x₂, ....,х_n, х_n+1), что еще более упростит принятую формулировку задачи и позволит сохранить неизменными используемые обозначения точек, множеств и т. п. (оптимальная величина ω, как и ранее, есть ω^* ≡ x^*_n+1).

Погрузив множество U_ω≡U в некоторый многогранник Q (для простоты - параллелепипед, заданный как a_j≤x_j≤b_j, j = 1,...., n+1), обратимся к задаче: найти Х = (х₁, х₂, ...., х_n+1)→max {x_n+1}, X∈Q. Искомый максимум (если он существует) будет достигнут в одной из крайний точек Q (см. гл. 1) (обозначим ее X̃). Прямая, проходящая через X̃ и X₁∈U₀, определяется уравнением X = X₁+a(X̃-X₁) и пересекает границу U в тех точках Х_Γ, которые удовлетворяют условиям X_Γ = X₁+а(Х̃-X₁), φ(Х_Γ) = 0, причем 0≤а_Β≤1 (рис. 4.2). Если в этой ситуации сравнить значения x_n+1 относящиеся к Х_Γ (здесь x_n+1+1 = x_(n+1)Γ) и X̃ (здесь x_n+1=х̃_n+1), с х^*_n+1 то окажется х_n+1≥х^*_n+1≥x_(n+1)Γ (замена U на Q означает расширение выбора допустимых X с перспективой улучшить достижимый экстремум целевой функции х̃_n+1). В дальнейшем естественно стремиться к сближению величин х̃_n+1 и x_(n+1)Γ с тем, чтобы последовательно уточнять оценку х^*_n+1. Сделать это можно путем от сечений каких-то частей многогранника Q гиперплоскостью, касательной к поверхности φ(Х) = 0 в точке Х_Γ (в результате Q будет все плотнее "охватывать" U, а погрешность определения x^*_n+1 уменьшаться).

Каждый шаг подобного процесса связан с необходимостью решать задачу линейного программирования с целевой функцией х_n+1 и системой ограничений, включающей не только первоначальные неравенства a_j≤x_j≤b_j (j = 1,....,n+1), но и ряд неравенств вида Δφ(Х_Γ)×(X-Х_Γ)≥0, учитывающих присутствие отсекающих гиперплоскостей (их число увеличивается на единицу после очередного шага). Получаемая невозрастающая последовательность значений х_n+1 (верхние оценки x̃^*_n+1) сходится при определенных условиях к решению исходной задачи нелинейного программирования; то же относится и к последовательности {x_(n+1)Γ}.

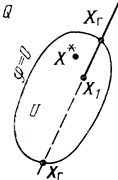
Рис. 4.2

Строгое доказательство сходимости рассматриваемого метода связано с предположениями о гладкости функций f(X), φ_i(Х), выпуклости множества U и т. п., что может не всегда иметь место ка практике. Тем не менее несомненным достоинством метода являются достаточность решения на каждом шаге только линейной задачи и возможность вычислять верхнюю и нижнюю оценки ω^* = x^*_n+1 (это позволяет ориентироваться в общей обстановке и довольствоваться во многих случаях приближенными результатами, не добиваясь сходимости вычислительного процесса к точному оптимуму).