4.6. Оптимизация на дискретных множествах. Метод ветвей и границ

Область определения задачи математического программирования часто имеет дискретную структуру (например, представляет собой совокупность конечного числа точек, линий, поверхностей); подобная ситуация рассматривалась в § 1.6, 1.7. В частных случаях удается выявить типичные геометрические признаки указанной совокупности (узлы целочисленной решетки, множества параллельных прямых и т. п.); в общем случае такие признаки отсутствуют, что затрудняет поиск решений соответствующих задач и приводит к необходимости применять различные комбинаторные методы, простейшим (и нежелательным) представителем которых является метод полного перебора вариантов.

Пусть дана задача: найти Х∈U→min{z = f(X)}, где U - дискретное множество. Предполагается, что U можно разбить на не пересекающиеся подмножества U₍₁₎, U₍₂₎,....,U_(η) причем способ разбиения должен выбираться применительно к конкретным условиям исследования; далее, нужно уметь оценить нижнюю границу значений г на каждом подмножестве U_(i)(i = 1,...,η) и найти, таким образом, ряд чисел ẑ_(i), обладающих свойством ẑ_(i)≤f(Х), Х∈U_(i) (здесь возникают самостоятельные задачи определения ẑ_(i)).

Если теперь допустить, что каждая подобласть U_(i) делится, в свою очередь, на новые U_(i,l) (1≤i≤η, l = 1,..., р) и существуют пути получения соответствующих ẑ_(i,l), то имеет смысл исследовать процесс ветвления (рис. 4.3) с целью выявить бесперспективные подмножества U и сократить за счет этого объемы вычислений. Идея направленного разбиения U с последовательными оценками ẑ_(i), ẑ_(i,l),... лежит в основе метода ветвей и границ.

Чтобы иметь возможность сравнивать между собой подмножества U_(i,l,..), заметим следующее: каким бы способом ни была найдена оценка ẑ, относящаяся к исходному U, она не ухудшится при рассматриваемых разбиениях, т. е. ẑ_(i)≥ẑ, (i = 1,...,η); точно так же ẑ_(i,l)≥ẑ_(i) (1≤i≤η; l = 1,..., р) и т. д. Чем больше расхождения между величинами правых и левых частей этих неравенств, тем менее перспективным представляется соответствующее под множество очередного уровня, однако необходимые выводы

могут быть сделаны только после вычисления всех ẑ_(i), затем ẑ_(i) всех при некотором фиксированном i, найденном на предыдущем шаге, и т. д. Результатом подобных действий является постепенное сужение области поиска X^*.

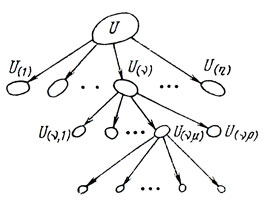
Рис. 4.3

Алгоритм метода включает следующие операции:

а) получение ẑ и выбор начальной точки X₀∈U (правила для этого формулируются применительно к конкретным условиям задачи; например, в целочисленном линейном программировании за величину z можно принять значение ẑ в точке X̂, а в качестве Х₀ использовать ближайшую к X̂ точку, удовлетворяющую требованиям целочисленности, см. п. 1.6);

б) сравнение ẑ с f(Х₀); если окажется f(X₀) = ẑ, то Х₀ = Х^* (это следует из определения ẑ); в противном случае - переход к п. в);

в) разбиение множества U на конечное число подмножеств U_(i), (i = 1,...,η) (способ разбиения заранее не. оговаривается);

г) получение оценок ẑ_(i) и выбор среди них

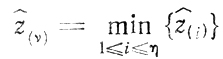
(этим однозначно определяется подмножество U_(υ), предназначаемое для дальнейших исследований);

д) выбор точки X₁∈U_(υ) (аналог Х₀) и сравнение ẑ_υ с f(X₁); если f(X₁)=ẑ_(υ), то Х₁ = Х^*; при f(Х₁)>ẑ_(υ) - переход к п. е);

е) разбиение U_(υ) на ряд подмножеств U_{(υ, l)} (l = 1,..., р), тем или иным способом;

ж) получение ẑ_{(υ, l)} и выбор среди них

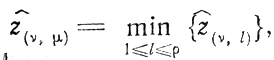
что позволяет указать U_{(υ, μ)};

з) выбор X₂∈U_{(υ, μ)} И сравнение ẑ_{(υ, μ)} с f(Х₂); в зависимости от результата -конец или продолжение процесса поиска X^* по рассмотренной схеме (см. рис. 4.3).

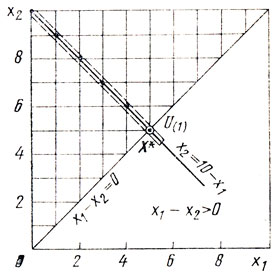
Рис. 4.4

Предложенный алгоритм обладает тем преимуществом, что не налагает никаких ограничений на структуру U и при удачных разбиениях позволяет эффективно исключать бесперспективные U_{(i, l,...)}. Вместе с тем разработка правил ветвления, способов получения очередных ẑ и Х_k (k = 1, 2, ...) может потребовать специальных исследований, отражающих специфику конкретных задач, но часто приводящих к отрицательным (в смысле экономии средств и времени) результатам.

Метод ветвей и границ хорошо зарекомендовал себя в решениях целочисленных линейных задач, ряда задач распределения ресурсов, однако в общем случае его применение требует осторожности. Ниже дан иллюстративный пример.

Пример: найти х₁, х₂→min {z = max(x₂, 10-x₁)} при х₁-x₂≤0; 0≤x₁, x₂≤10, x₁, x₂ - целые числа.

Решение: в выражении целевой функции под знаком максимума собраны неотрицательные величины, поэтому очевидная оценка ẑ есть 0; за Х₀ здесь можно принять точку (0,0), принадлежащую области определения задачи (рис. 4.4). Поскольку f(0, 0) = max {0, 10} = 10>ẑ, необходимо начать разбиение U. Множество U (порядка 60 узлов решетки, рис. 4.4) разделим на два подмножества - точки, лежащие на прямой х₂ = 10-х₁ и все остальные точки (это облегчает вычисления ẑ). Таким образом U₍₁₎ включает (0,10), (1,9), ..., (5,5) и ̂₍₁₎ = 5; для всех X∈U₍₂₎ выполнены условия: либо x₂<10-x₁ либо x₂>10-x₁, т. е. f(X)≥6 = ẑ₍₂₎; следовательно, ẑ₍₂₎<ẑ₍₁₎ и дальнейший анализ должен проводиться применительно к U₍₁₎.

Подмножество U₍₁₎ содержит всего 6 элементов, и они уже исследованы; здесь X₁ = (5,5); f(X₁) = ẑ₍₁₎ = 5, поэтому Х^* = (5,5), z^* = 5.

Основные идеи и принципы построения схем поиска X^*, r^* в задачах с полной информацией применимы и к задачам с неполной информацией, изучаемым в гл. 5-7, хотя специфика условий, в которых проводятся исследования, существенно влияет на способы получения решений.