Глава пятая. Поиск экстремума в условиях неопределенности. Простейшая задача

5.1. Роль эксперимента в исследованиях. Принцип гарантированного результата

Методы решения задач математического программирования, рассмотренные в предыдущих главах, предполагали проведение целого ряда исследований, связанных с изучением особенностей той или иной задачи, различного рода доказательствами, построением вычислительных схем и т. п. Основой всего этого служило четкое представление о характере зависимости z = f(X).

Несмотря на большие успехи теории математического программирования, еще многие оптимизационные задачи не решены в общем виде. Примеры таких задач можно найти при исследовании систем, деятельность которых не поддается формальному описанию, при оценке наилучшего поведения человека в определенных ситуациях и т. д. Учитывая эти замечания, обратимся к изучению задач, для которых характерно следующее:

а) целевая функция не имеет аналитического выражения;

б) значения этой функции при тех или иных значениях X могут быть получены посредством проведения некоторой операции, которая в дальнейшем будет называться экспериментом (здесь имеет смысл расширить понятие "эксперимент", считая, что экспериментом являются и обращение к таблице или памяти ЭВМ, и наблюдение результата на экране моделирующей установки, и непосредственное проведение каких-либо измерений или вычислений и т. п.);

в) представляющее интерес максимальное или минимальное значение целевой функции и соответствующие точки X^* могут быть получены путем проведения ряда однородных экспериментов, число которых ограничено.

Указанные действия составляют процесс поиска экстремума z = f(Х) в рассматриваемых специфических условиях. Правила, по которым ведется поиск, называются стратегиями. Поскольку в рамках одной и той же задачи можно применять различные стратегии поиска X^*, z^*, естественно попытаться найти ту из них, которая:

является наилучшей в смысле уменьшения объема необходимых вычислений, поэтому наряду с главным требованием- найти точку экстремума г - возникает дополнительное (но не менее важное) требование выбора стратегии поиска, обладающей нужными свойствами.

Конечно, такой подход возможен и в случаях, когда вид зависимости z = f(X) известен, но аналитические методы решения по каким-либо причинам не удается применить. Следовательно, замечание а) нужно рассматривать скорее как указание на то, что существует обширный класс задач, которые могут быть решены несмотря на препятствие, кажущееся на первый взгляд непреодолимым.

Рис. 5.1

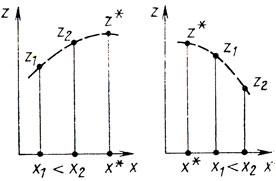
Рис. 5.2

Чтобы лучше представить себе основные идеи, связанные с организацией поиска, обратимся к анализу детерминированных схем. Здесь в первую очередь рассматривается случай скалярного аргумента (простейшая задача поиска).

Предположим, что X = (x₁) и целевая функция обладает такими особенностями:

- имеет только один максимум (относительный, он же и абсолютный) на интервале определения (свойство унимодальности, см. рис. 5.1);

- может не удовлетворять требованиям непрерывности, существования производной во всех точках и т. п.

Всегда можно считать, что x₁ меняется в пределах ют 0 до 1 (любой другой интервал изменения x₁ легко приводится к [0, 1]); кроме того, в дальнейшем удобно опустить индекс "1", так что х₁ = х.

Чтобы иметь возможность использовать свойство унимодальности, обратимся к определению. Пусть х₁ и х₂ есть значения х в двух экспериментах, дающих соответственно z₁ и z₂, а х^* - значение х, при котором достигается max z = z^* (полагаем х₂>х₁). Функция z = f(x) является унимодальной, если из условия х₁>х^* следует z₁>z₂, а из условия х₂<х^*-z₁<z₂ (рис. 5.2). Таким образом, если точки х₁ и х₂ расположены по одну сторону от х^*, то более близкой к х^* точке отвечает большая величина z. Определение исходит из возможности найти z при данном х только путем эксперимента и поэтому не затрагивает никаких свойств функции z = f(x). Это, в свою очередь, позволяет прийти к важному выводу: результат любой пары экспериментов должен указать такой интервал значений х, который по своей величине меньше исходного интервала [0, 1] и обязательно содержит х^*.

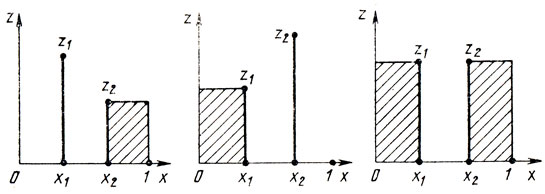
Рис. 5.3

Действительно, до проведения экспериментов было известно, что 0≤x^*≤1. Если х₁ и х₂ выбраны из условия х₁<х₂ и для каждого из них получена соответствующая величина г, то возможны три варианта соотношений между z₁ и z₂: z₁>z₂, z₁<z₂, z₁ = z₂ (рис. 5.3). При z₁>z₂ точка х^* не может лежать правее точки х₂ (иначе нужно требовать z₁<z₂), и под интервал [х₂, 1] должен быть исключен из рассмотрения. Далее, при z₁<z₂ точка х^* не может находиться левее x₁ (иначе z₁>z₂). Наконец, при z₁ = z₂ точка х^* должна находиться между x₁ и х₂. Любой из найденных подынтервалов, содержащих х^*, меньше исходного интервала [0, 1]. Таким образом, использование принятого выше определения унимодальности позволяет организовать пошаговый процесс последовательного сужения указанных подынтервалов с тем, чтобы в конце концов приблизиться к х^*.

Для получения формальных зависимостей обратимся к общему случаю произвольного числа экспериментов N, находящихся в распоряжении исследователя (N>2). Схема, отражающая возможные исходы этих N экспериментов, строится по принципу: варианту с номером q(\^q^N) соответствует предположение о том, что наибольшее z найдено в точке х_q (рис. 5.4). Определение интервалов, на которые должно приходиться значение х^*, происходит здесь так же, как в примере с N = 2 (рис. 5.3). Соотношение величин z_q-1 и z_q+1, получаемых в точках, соседних с x_q(q = 1,...., N), не влияет на результат (безразлично, будет ли z_q-1>z_q+1 или z_q-1<z_q+1; важно, чтобы z_q было наибольшим из всех z найденных при данном N). Из рис. 5.4 видно, что длина и положение рассматриваемых интервалов меняются в зависимости от величины q, значений x₁, х₂, .....,x_N, выбираемых при каждом q = const (т. е. стратегии поиска), и от числа N. Формально это отражено в неравенствах

которые справедливы для всех названных q, если точки x = 0 и х = 1 обозначены как х₀ и x_N+1.

Неравенства (5.1) позволяют ввести меру эффективности поиска и определить на этой основе рациональные схемы его организации. Назовем интервал [x_q-1, x_q+1] интервалом неопределенности; его длина l_N = x_q+1-x_q-1 при известном N зависит от исхода всех N экспериментов, дающего номер q, и самих х₁, х₂, ....,x_N, выбранных из тех или иных соображений, т. е. l_N = ln (k, q) (здесь символом % обозначена вся совокупность х₁, х₂, ...., x_N).

Чтобы определить рациональную стратегию (или ее начальную фазу) заранее, не приступая к экспериментам, достаточно рассмотреть следующие условия: если x₁, x₂, .....,x_N выбраны и тем самым задан ряд интервал лов [x_q-1, x_q+1] (q = 1,..., N), то какой-то из них имеет наибольшую (по сравнению с остальными) длину l_N=l̄_N. Приняв l̄_N в качестве характеристики выбранной совокупности χ = (х₁, х₂,...,x_N), можно быть уверенным в том, что реальный результат поиска х^* при этих x₁ х₂, ..., x_N, оцениваемый величиной l_N, будет лучше (или по крайней мере не хуже) l̄_N. Очевидно, l_N, заданная как

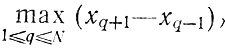
является функцией только χ (принятая ориентация на худший случай дает гарантию от непредвиденных осложнений, которые могут возникнуть в ходе проведения экспериментов). Если теперь рассмотреть множество стратегий с показателями l̄_N, то лучшей из них следует признать ту, которой соответствует наименьшая величина l̄_N (преимущество такого выбора в том, что, во-первых, сохраняется гарантия получить реальную длину интервала неопределенности, не превышающую l̄_N, и, во-вторых, эта гарантированная длина минимальна). Обозначив рассматриваемый минимум l̄_N как L_N, получим

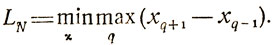(5.2)

Величина L_N определяет единственную стратегию, называемую минимаксной. Всякое отклонение от нее приведет лишь к опасности ухудшения результата будущего поиска. Большое преимущество использования критерия L_N заключается в возможности априорного выбора оптимальной стратегии действий, приводящих к получению х^*, z^*.

Существует два вида стратегий: пассивные, в которых еще до начала эксперимента назначены все x₁, x₂, ....., x_N, и активные, в которых выбор очередных значений х зависит от результатов предшествующих экспериментов (имеет место накопление и активное использование информации о свойствах целевой функции).