5.2. Пассивные стратегии поиска. Оценка приближения к оптимуму

Переходя к рассмотрению различных методов поиска х^*, z^*, необходимо выяснить, каким образом могут быть найдены схемы, позволяющие получать L_N в виде (5.2). Это удобно сделать прежде всего применительно к случаю N = 2.

Пусть х₁ и х₂ - значения х в двух экспериментах, причем 0≤х₁<х₂≤1. Очевидно, длина l̄_N = l̄₂ представляет собой в данном случае наибольшее значение двух разностей х₂-х₀ и x₃-x₁, где х₀ и x₃ равны соответственно нулю и единице.

Таким образом,

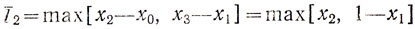
Исследовать l̄₂ как функцию переменных х₁, х₂ удобнее всего путем построения линий l̄₂ = const на плоскости x₁, x₂; эти линии показаны на рис. 5.5. По условиям выбора оптимальной стратегии нужно среди полученных l̄₂ найти min l̄₂ = L₂.

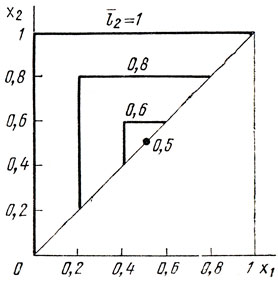
Рис. 5.5

Таковым является L₂ = 0,5 (при x₁ = x₂ = 0,5). Принять эти x₁ и х₂ в качестве "рабочих" значений нельзя,поскольку оказалось нарушенным требование x₁<х₂. Чтобы обойти это затруднение, введем величину ε-минимальное значение разности х₂-x₁, при котором еще различимы z₂ и z₁ (своего рода чувствительность метода). Тогда, положив x₁ = 0,5-ε/2, x₂ = 0,5+ε/2, можно обеспечить и различение z₁, z₂, х₁, х₂, и минимизацию l̄₂. Следовательно, искомая стратегия и гарантированный результат определяются как

^{x₁ = (1 - ε) /2, x₂ = (1 + ε)/2, L₂ = (l + ε)/2. (5.3)}

Стратегию (5.3) обычно называют ε-минимаксной.

Перейдем теперь к случаю N = 3. Как я прежде, полагаем 0≤x₁<x₂<x₃≤1, x₀ = 0, x₄ = 1; здесь уже три интервала [х₀, х₂], [х₁, x₃], и [х₂, х₄] подлежат сравнению с целью определения величины l̄₃ = max{x₂, x₃-x₁, 1-x₂}, являющейся функцией трех переменных. Чтобы дать наглядную картину изменений l̄₃, достаточно рассмотреть линии l̄₃ = const на плоскости x₁, х₂ при фиксированных х₃. Если x₃ = 1, они полностью совпадают с линиями, построенными на рис. 5.5; если же х₃<1 (например, х₃ = 0,9; 0,7; 0,5), то картина меняется (рис. 5.6), однако ясно, что, во-первых, нельзя ожидать появления x₃<0,5 (при x₁<x₂<x₃) и, во-вторых, всегда нужно назначать x₂ = 0,5 (это возможно, конечно, при ε<0,25).

Таким образом, для случая N = 3 существует множество минимаксных стратегий:

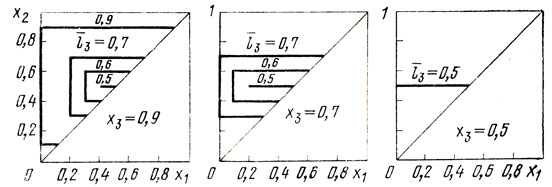
Рис. 5.6

Сравнивая (5.4) и (5.3), можно видеть, что разность L₂-L₃ составляет всего 0,5ε, поэтому схема трех экспериментов при малых ε (понятие "малые" уточняется в каждом конкретном случае) не дает практически выигрыша в величине L_N.

Естественно возникает вопрос: как построить минимаксную схему поиска х^*, z^* при произвольном, числе экспериментов N>3? Из предыдущих оценок следует, что, во-первых, N не может превысить величины [1 + 1/ε], если соблюдается ε-ограничение, и, во-вторых, с увеличением N варьирование значений х становится почти невозможным. Вместе с тем формирование ε-минимаксной стратегии облегчается хотя бы в том плане, что становится легче выбрать стратегию на основе "здравого смысла" и показать, что она является минимаксной, чем исследовать условия ее существования. В связи с этим рассмотрим стратегию поиска однородными парами (она применима в случаях, когда N четное).

Схема строится следующим образом (рис. 5.7): N значений х разбиваются на пары (х₁, х₂), (x₃, x₄), ... ..., (x_N-1, x_N) так, что величины разностей x_q-x_q-1 (q = 2, 3, ..., N) постоянны и равны ε; далее, интервал [0, 1] делится на N j 2+1 равные части (т. е. на отрезки длиной 2/(2+N)), и пары (x_q-1, x_q) размещаются с условием, чтобы точки деления попали между соответствующими x_q-1, x_q (при этом требуется сохранить расстояние между x_q с четными индексами постоянным и равным 2(1+ε)/(N+2)). Такое размещение точек х₁, х₂, ...., x_N всегда возможно, так как разность

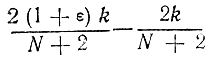
не превышает ε при любых допустимых k (здесь k - номер очередной пары, 1≤k≤N/2).

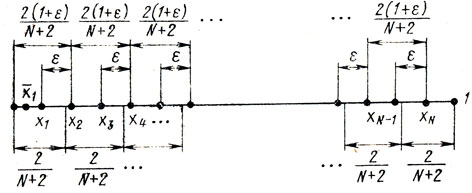
Рис. 5.7

Стратегия поиска однородными парами является ε- минимаксной, в чем можно убедиться, смещая любую из точек х₁, х₂,..., x_N. Например, если x₁ займет положение x̄₁ (рис. 5.7), то интервал [х̄₁, х₃] будет больше, чем [х₁, x₃], и за счет этого увеличится l̄_N, что недопустимо. Точно так же нельзя приблизить х₂ к х₃ из-за опасности расширения интервала [х₀, х₂] и т. д. Эффективность рассмотренной схемы оценивается величиной

Теперь остается исследовать случай нечетного N. Поступим здесь так: точки с четными номерами расставим через равные промежутки длиной 2/(N+1), а точки с нечетными номерами - между четными точками так, чтобы расстояния x₃-x₁, x₅-x₃,....., x_N-x_N-2 находились в пределах от 2ε до 2/(N+1) (рис. 5.8). Последнее условие означает, во-первых, что L_N зависит здесь только от положения точек с номерами 2, 4, ..., N-1 и, во-вторых, что существует множество оптимальных стратегий, отличающихся друг от друга значениями координат нечетных точек. Таким образом, L_N = 2/(N +1). В том, что схема рис. 5.8 является ε-минимаксной, можно убедиться, изменив любое х с четным номером (l̄_N возрастает).

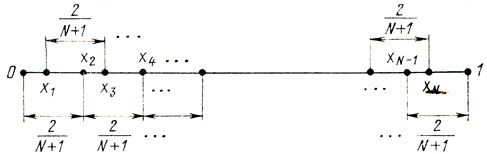
Рис. 5.8

В заключение заметим, что предложенные стратегии реализуются, если при данном ε число N выбрано должным образом.