6.4. Методы организации переходов. Требуемые свойства целевой функции

Идеи, лежащие в основе построения стратегий поиска X^*, z^* при n>2 (этап II), весьма разнообразны. Часто они формируются применительно к конкретным условиям задачи, однако существуют методы, претендующие на универсальность и применимые к решению классов задач.

Метод исключения

По своему содержанию метод исключения схож с теми схемами поиска, которые были изучены в гл. 5. Он предполагает последовательные отсечения отдельных частей области эксперимента плоскостями, касательными к поверхностям уровня. Основание для этого дает информация, получаемая в периодически повторяемых локальных исследованиях окрестностей опорных точек.

Пусть на какой-либо поверхности уровня выбрана опорная точка, через которую прошла касательная плоскость (гиперплоскость) , разделившая область эксперимента на две подобласти (рис. 6.5). Если f(X) строго унимодальна, то оказывается возможным отделить подобласть с более высокими (т. е. лучшими) значениями z от подобласти с меньшими z, не представляющей интереса. В результате образуется новая область неопределенности, и применительно к ней вся процедура исключения повторяется. Сделав несколько таких шагов, можно приблизиться к X^* и завершить процесс поиска исследованиями по программе этапа III.

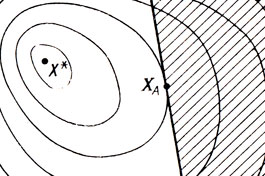
Рис. 6.5

Формальным обоснованием метода исключения служит следующая теорема (15):

если максимум строго унимодальной функции z=f(X) достигается в точке Х^* = (x^*₁, x^*₂ ,..., х^*_n), то для любой точки X_A = (x_1A, x_2А,...., x_nA) из области, эксперимента справедливо соотношение

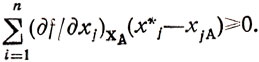
Доказательство: предположим противное -

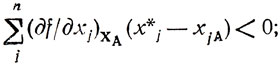
пусть X - точка, лежащая на отрезке, соединяющем Х_А с X^*; ее координаты заданы равенствами x_j = ax^*_j+(1-a)x_ja(j=1,...,n; 0<a<1); поскольку положение X заранее не оговорено, его всегда можно выбрать так, что будет справедливо утверждение

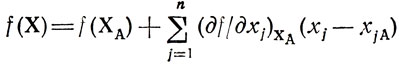
или

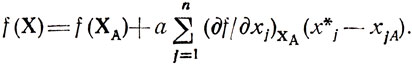
Величина а положительна, а сумма, умножаемая на а, меньше нуля (по предположению), следовательно, f(X)<f(X_A); но этого не должно быть, если f(X) строго унимодальна (возникшее противоречие доказывает теорему). □

Обращая внимание на тот факт, что

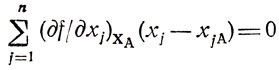
есть уравнение гиперплоскости, касательной к поверхности уровня в точке Х_А, приходим к заключению: доказанная выше теорема утверждает необходимость появления X^* всегда по одну сторону от касательной.

Достоинством рассматриваемого метода является простота; на основании только одного локального исследования окрестности очередной опорной точки (оно нужно для определения положения касательной) отбрасывается целая бесперспективная область. Недостатки метода-ограниченные возможности применения (только для строго унимодальных f(X)) и чувствительность к ошибкам эксперимента (они пока не принимаются во внимание). Ниже дан иллюстративный пример; несмотря на свою простоту он позволяет продемонстрировать

технику применения метода.

Пример: найти значения переменных х₁, х₂ х₃, доставляющие максимум строго унимодальной функции z = е^{-(0,1x2₁+0,4x2₂+0,9x2₃)} при условиях 0≤x_j≤3 (j = 1,.., 3), ε = 0,05.

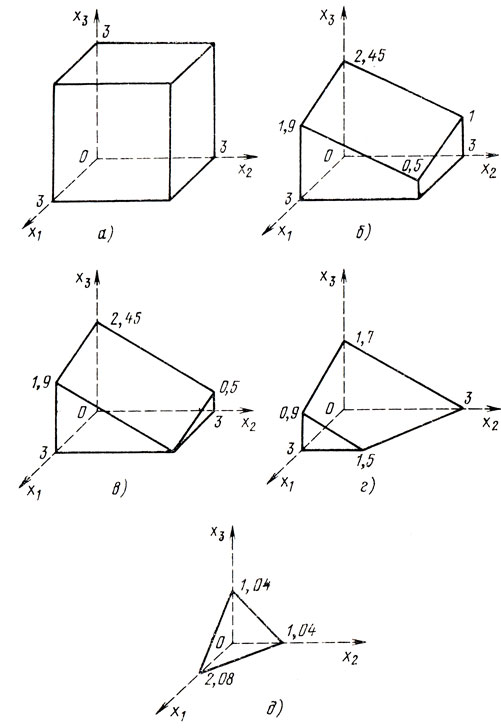
Рис. 6.6

Решение: а) областью эксперимента Э является в данном случае куб (см. рис. 6.6,а). В качестве начальной опорной точки выбирается средняя точка Х_с (центр куба) с координатами x_1c=1,5, х_2с=1,5, x_3с=1,5. Значение z в этой точке есть z_c=e^-3,15. Проводится группа пробных экспериментов в точках X_1c=(1,55; 1,5; 1,5),

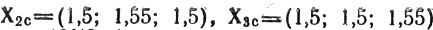
с целью оценки

производных (df/dx_j)_Xc и составления уравнения касательной.

Результатами этих экспериментов являются соответственно

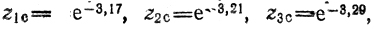
позволяющие получить

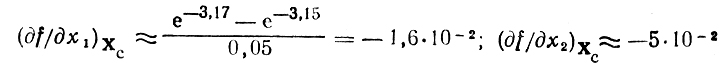
и

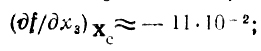
отсюда следует уравнение касательной

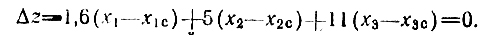
Для дальнейшего рассмотрения интерес представляют точки, удовлетворяющие условию Δz≥0, которое вместе с исходными условиями 0≤x_j≤3 дает возможность указать новую область неопределенности (см. рис. 6.6,6), остающуюся после проведенного первого исключения.

б) использование средней точки в качестве центра области оказалось удачным (отброшена почти половина Э), поэтому, начиная второй шаг, будем опять ориентироваться на среднюю точку как на новый центр группы пробных экспериментов; обозначая его Х_ц, получаем x_1ц = 1,5; x_2ц = 1,5; x_3ц = 1,2; z_ц = е^-2,42 (полезно заметить, что z_ц>z_с, т. е. "движение" происходит в нужном направлении). Значения z в точках Х_1ц = (1,55; 1,5; 1,2), Х_2ц = (1,5; 1,55; 1,2) и Х_3ц = (1,5; 1,5; 1,25) равны соответственно

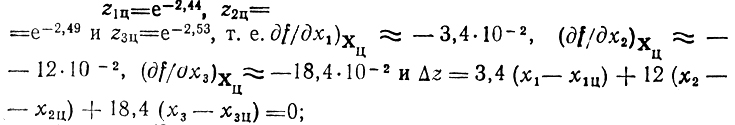
как и в предыдущем случае, условия Δz≥0, 0≤x_j≤3 позволяют прийти к новой области неопределенности, показанной на рис. 6.6в.

Второе исключение оказалось не таким эффективным, как первое; причина этого - смещение точки Х_ц к периферии области Э (здесь проявился один из скрытых недостатков выбора средней точки в качестве центра), поэтому на третьем шаге придется внести необходимые коррективы.

в) Пусть центром оставшейся области неопределенности (рис. 6.6,в), имеющей объем V, будет ее центр тяжести Х_цт, координаты которого заданы известными формулами

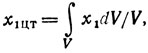
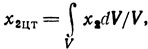
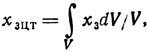
дающими

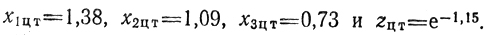
Точки проведения пробных экспериментов есть Х_1цт (1,43; 1,09; 0,73), Х_2цт = (1,38; 1,14; 0,73) и Х_3цт = (1,38; 1,09; 0,78). Соответствующие результаты:

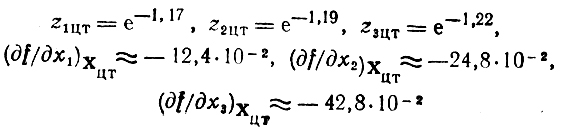
и

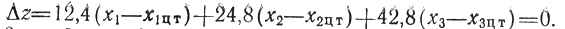
Условий Δz≥ и 0≤x_j≤3 указывают область неопределенности, представленную на рис. 6,6,г. Легко видеть, что выбор Х_цт в качестве центра оправдал себя; прежде чем сделать следующий шаг, имеет смысл проанализировать то, что уже достигнуто; при переходах из Х₀ в Х_ц и далее в Х_цт значения z возрастали, и наиболее существенное увеличение z произошло на переходе Х_ц→Х_цт. Рассмотрим произвольную точку X на продолжении отрезка, соединяющего Х_ц с Х_цт, предполагая, что это будет продолжение строго возрастающей прямолинейной траектории, идущей в X^*. Учитывая неравенства x_jцт<x_jц(j = 1, 3), исследуем те X^*, координаты которых (X_j) связаны с координатами Х_ц и Х^цт соотношениями x_jцт = ax_jц+(1-a)x_j (j = 1, 3; 0<a<1), поскольку именно таким X будут отвечать величины z, превышающие z_цт. Очевидно, прямая, продолжающая отрезок [Х_цт, Х_ц] и содержащая точку X, должна где-то пересечь границу области, показанной на рис. 6.6.г, причем это будет либо граница x₁ = 0, либо x₂ = 0, либо x₃ = 0.

Полагая в равенстве, связывающем координаты Х_ц, Х_цт, X, поочередно равными нулю x₁, х₂, х₃, получаем из него три значения а, меньшее из которых, т. е.

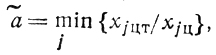
определяет искомую точку пересечения. В нашем случае ã = 0,606, следовательно, точка пересечения есть Х_п = (1,17; 0,45; 0). Проведя в точке Х_п эксперимент (т. е. вычислив

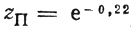
убеждаемся в том, что действительно существует прямолинейная строго возрастающая траектория, проходящая через Х_ц, Х_цт и Х_п, однако вопрос о местонахождении X^* останется открытым.

г) Поскольку наибольшей из всех полученных z является z_Π, можно принять точку Х_п за новый центр группы пробных экспериментов и провести все необходимые операции, т. е. найти

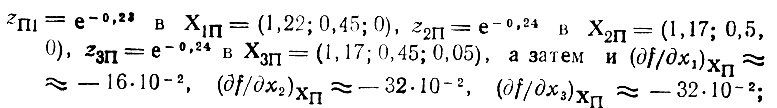
уравнение касательной плоскости Δz = 16 (x₁ - х_1П) + 32 (х₂ - x_2П) + 32 (х₃ - х_3П) вместе с исходными ограничениями и требованием Δz≥0 укажет новую область неопределенности (см. рис. 6.6,д); ее объем составляет менее 40% объема предыдущей области (рис. 6.6,г), что является следствием анализа обстановки, проведенного перед четвертым шагом (теперь выяснилось, что Х_п не есть X^*). Обратим внимание на следующее обстоятельство: в процессе переходов от одной опорной точки к другой значения каждой их координаты не увеличивались (x_jc ≥ x_jц > x_jцт > x_jΠ, j = 1,3). В этой ситуации имеет смысл проверить точку (0,0,0), которая к тому же является крайней в области эксперимента; вычисляем z (0,0,0) = 1; все предшествующие z были меньше, поэтому можно предположить Х^* = (0,6,0), z^* = 1 и перейти к заключительному этапу решения задачи.

д) Прежде всего необходимо построить простейшую аппроксимирующую формулу (модель поверхности отклика в окрестности X^*); для этого находим значения z в точках

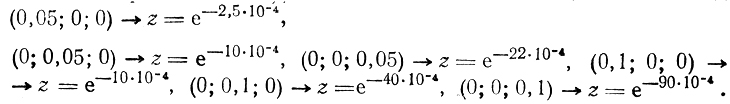
Затем даются оценки производных

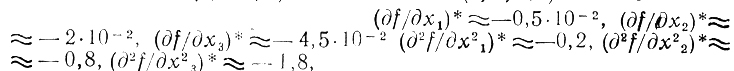
выступающие в роли коэффициентов формулы

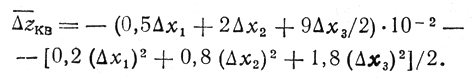
Составляется система уравнений

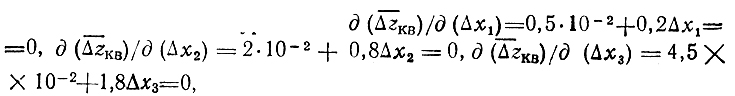
решения которой

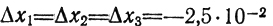
удовлетворяют неравенствам |Δx_j|<ε. Таким образом, формула для Δz_KB может быть признана допустимой, тем более что Δz_KB как функция Δx_j (j = 1,3) является отрицательно определенной (в условиях рассматриваемой задачи); вопрос о замене точки Х^* = (0,0,0) точкой Х^** = (0,025; 0,025; 0,025) в данном случае непринципиален.

Метод наискорейшего спуска

Приступая к изучению этого метода, необходимо иметь в виду, что я представляет собой скалярную функцию векторного аргумента Х = (х₁, х₂, ....,х_n).

Ее модели, используемые на разных этапах поиска X^*, z^* и основанные на оценках частных производных первого и высших порядков, позволяют предполагать существование вектора градиента ∇f = (df/dx₁, df/dx₂, ....,df/dx_n) в точках Х∈Э.

Чтобы выяснить, какую роль играет градиент в выборе способа переходов от одной опорной точки к другой, обратимся к формуле производной по направлению:

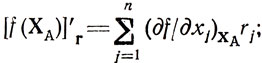
здесь r-единичный вектор с составляющими r_j(j= 1,...,n), в направлении которого берется производная функции z = f (X) в точке Х_А. Правая часть этого равенства есть скалярное произведение векторов ∇f, r, определяемое и как |∇f_А||r| cos Θ или |∇f_A|cosΘ, где ∇f_A - градиент f(X) в Х_А, Θ - угол между ∇f_A и r.

Ясно, что наибольшая величина производной достигается при Θ=0, т. е. тогда, когда направление r совпадает с градиентным. Таким образом, шаг в направлении ∇f означает возможность получить максимальное (по модулю) приращение z.

Эта идея лежит в основе любого градиентного метода, в том числе и метода наискорейшего спуска (возникновение названия связано с задачей отыскания min z, см. 4.3). Учитывая, что вектор ∇f всегда перпендикулярен поверхности уровня в точке, где он рассматривается, можно представить процесс переходов в следующем виде: из очередной опорной точки, в которой с помощью пробных экспериментов найдены составляющие ∇f, делается шаг в градиентном направлении; величина шага определяет новую опорную точку, применительно к которой вся процедура повторяется. В результате образуется ломаная траектория "движения" к X^* (рис. 6.7), воспроизводящая более или менее приближенно непрерывную "чисто градиентную" траекторию.

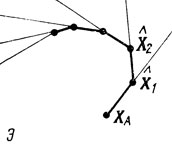
Рис. 6.7

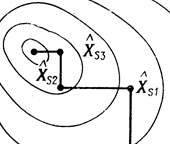
Рис. 6.8

Методу наискорейшего спуска посвящено много работ, поэтому здесь достаточно ограничиться изучением вопроса о выборе длины шага при переходах от одной опорной точки (например, Х_А) к другой. Рассмотрим уравнение луча, исходящего из Х_А в направлении ∇f_A : Х = Х_А+a∇f_А, a>0 или x_j-x_JA+a(df/dx_j)_XA (j = 1,...,n). Если подставить последнее равенство в выражение

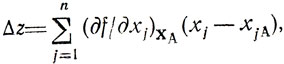
определяющее линейную часть приращения z, то полученная формула

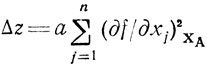
покажет, что с ростом а (т. е. при "движении" вдоль ∇f_A) всегда появляются положительные Δz (пусть на достаточно малом шаге, в пределах допустимости линейной оценки Δz). Очевидно, перемещение вдоль луча имеет смысл до тех пор, пока значения z улучшаются. Отсюда следует рекомендация: продолжив луч от исходной точки Х_А до пересечения с границей области эксперимента, необходимо организовать на образовавшемся отрезке поиск точки экстремума функции z = f(X) любым из доступных методов (см. гл. 5). Найденная при этом оптимальная величина а=а̂ укажет точку Хь которая может быть принята в качестве новой опорной точки и т. д. (рис. 6.7). Таким образом, процесс решения задачи сводится к повторениям однотипных простейших операций поиска.

Метод наискорейшего спуска применим в случаях, когда f(X) унимодальна (а не только строго унимодальна), а также при ошибках эксперимента.

Метод Гаусса - Зайделя

В основе метода Гаусса - Зайделя лежит идея так называемого покоординатного поиска. Пусть из n переменных x₁, х₂, ..., х_n выбрана какая-то одна x_s(1≤s≤n), значения же остальных фиксированы (тем самым определена прямая, параллельная одной из координатных осей, а именно оси x_s). Производится поиск вдоль этой прямой (конечно, на том ее отрезке, который лежит в пределах области Э), в результате чего становится возможным указать точку экстремума X̂_s, функции z, еще не претендующую на роль X^*. После этого номера

меняется на р (1≤p≤n, p≠s), X̂_s назначается опорной точкой, и применительно к хр вся процедура повторяется. Так продолжается до тех пор, пока не будет найдена точка, подозрительная на экстремум (рис. 6.8). Полезно заметить, что одна и та же переменная x_s (или x_p) может быть исследована более одного раза.

Достоинства излучаемого метода: простота и отсутствие локальных исследований окрестностей опорных точек. Недостаток: ограниченные возможности применения (метод применим тогда, когда зависимость между переменными x₁, х₂, ..., х_n практически отсутствует). В связи с этим имеет смысл упомянуть об одном осложнении, часто возникающем на практике. Предположим,

что первый шаг привел к отысканию X_s; может оказаться, что попытка сделать следующий шаг будет неудачной какая бы переменная ни выбиралась в качестве свободной на втором шаге, значения z улучшить не удается, хотя достоверно известно, что X̂_s не есть X^*. Множество точек, из которых невозможно продолжить процедуру Гаусса - Зайделя, называется гребнем. Гребень не только частная специфическая особенность той или иной функции f(X); он может возникнуть, например, при повороте координатных осей, его появлению способствует ограниченная разрешающая способность экспериментов, выражающаяся в существовании конечного ε>0, и т. д.

Идея покоординатного поиска, как будет показано ниже, используется частично и в других методах.

Метод конфигураций

Пусть X₁₀ = (x₁₀, x₂₀, ..., х_n0)-точка, из которой начинается поиск, a Δx_j>s - выбранные заранее величины изменений соответствующих x_j (j = 1, ...,). Предлагается последовательность действий, предусматривающая поочередные изменения координат Х₁₀ с целью получения лучших (по смыслу задачи) значений z. Она заключается в следующем (на примере отыскания max z):

а) Выбирается переменная х₁ и оценивается (при известном Δх₁) значение целевой функции z = z₁₁ в точке Х⁺₁₁ = (х₁₀+Δx₁, x₂₀, ..., х_n0). Оно сравнивается со значением z = z₁₀, найденным предварительно в x₁₀; если оказывается z⁺₁₁ > z₁₀, то совершается переход из Х₁₀ в Х⁺₁₁, после чего Х⁺₁₁ обозначается просто как X₁₁; если же z⁺₁₁>z₁₀, проводится б).

б) Определяется z = z^-₁₁ в точке Х^-₁₁ = (х₁₀-Δх₁, x₂₀,... ...,x_n0). Если в результате сравнения z^-₁₁ с z_l0 оказалось z^-₁₁>z₁₀, то совершается переход из Х₁₀ в Х^-, обозначаемую как Х₁₁. Если же z^-₁₁≤z₁₀, то приходится признать неудачной попытку увеличения z за счет варьирования x₁ и перейти к рассмотрению х₂. Здесь роль исходной точки будут выполнять либо Х₁₁, либо Х₁₀ в зависимости от результатов операций а), б). В целях унификации обозначений удобно всегда использовать для этой точки обозначение Х₁₁, даже если ею является Х₁₀, т. е.

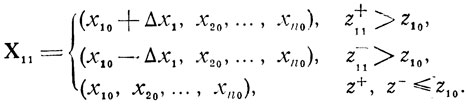
в) Оценивается значение z = z⁺₁₂ в точке Х⁺₁₂, которая определяется либо координатами (x₁₀+Δx₁, х₂₀+Δx₂, х₃₀, ...,х_n0), либо (х₁₀-Δx₁, х₂₀+Δх₂, х₃₀,..., х_n0), либо (x₁₀, x₂₀ + Δх₂, х₃₀,..., х_n0). Оно сравнивается со значением z в Х₁₁; если z⁺₁₂>z₁₁, то совершается переход из X₁₁ в X⁺₁₂ после чего точка Х⁺₂₁ обозначается как Х₁₂; если же z⁺₁₂≤z₁₁, проводится операция г).

г) Рассматривается точка Х^-₁₂, заданная аналогично Х⁺₁₁, но со второй координатой х₂-Δх₂. Величина z^-₁₂ сравнивается с z₁₁; если z^-₁₂>z₁₁, то совершается переход из точки Х₁₁ в Х^-₁₂, обозначаемую как Х₁₂; если же то Х₁₁ сохраняется в качестве исходной для последующих операций, связанных с х₃. Таким образом, в результате этих действий будет указана точка

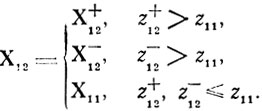
д) Описанная процедура повторяется для х₃, х₄, ... ..., х_n и позволяет получить точки X₁₃, X₁₄, ..., X_1n; с получением X_1n становится возможным указать первую конфигурацию (совокупность точек Х₁₀ и X_1n) и завершить тем самым первый цикл поиска X^*, z^*.

Чтобы начать второй цикл, необходимо указать новую исходную точку Х₂₀. Ею могла бы быть Х_1n, однако для ускорения процесса часто используется следующий прием: точки Х₁₀ и X_1n соединяются отрезком, и на его продолжении выбирается Х₂₀, причем расстояние между X_1n и Х₂₀ зависит от конкретных условий задачи. После того как Х₂₀ определена, все операции, перечисленные в пп. а)-д), повторяются сначала; в результате отыскивается точка Хоп, образующая вместе с Х₂₀ вторую конфигурацию, затем строится точка Х₃₀, являющаяся исходной для третьего цикла поиска, и т. д.

Ясно, что переход от X_k0 к X_k+1,0 (k - номер цикла) возможен тогда, когда Х_k0≠X_kn. Если оказалось Х_k0 = X_kn и, следовательно, Х_k+1,0 = Х_k0, то допустимы два предположения: либо точка Х_k0 находится на гребне, либо она представляет собой X^*. В этих условиях рекомендуется уменьшить Δx_j, j = 1,...,n (конечно, в рамках требований Δx_j≥ε), что позволит несколько "сузить" гребень (в случаях, когда остановка произошла из-за него) и продвинуться дальше в решении задачи. Если подобная операция не приводит к успеху, то поиск можно считать законченным, после чего остается провести исследования окрестности точки X^* (см. § 6.3).

Достоинством рассмотренного метода является простота локальных исследований поверхности отклика. Недостатки заключаются в некоторой громоздкости схемы переходов и неполноте информации, получаемой в процессе решения задачи (исследуются только направления, параллельные координатным осям). Ниже дан пример применения метода конфигураций.

Пример: найти значения переменных x₁ и х₂, доставляющие минимум функции z = 5x²₁-6x₁x₂+5x²₂+8x₁+24x₂+32 при ε = 0,05, Δx_j = 0,15 (j = 1,2).

Решение: а) областью эксперимента в данном случае является вся плоскость х₁, х₂ в качестве исходной точки может быть выбрана Х₁₀ = (0,0); для нее z₁₀ = 32. Первый шаг предполагает оценку z в точке Х⁺₁₁ = (0,15; 0); проведя соответствующие вычисления, получим z⁺₁₁ = 33,3 > z₁₀, что должно быть признано неудовлетворительным (здесь задача на отыскание min z).

б) Обращаемся к Х^-₁₁ = (-0,15; 0); для нее z^-₁₁ = 30,9 <210, поэтому Х>₁₁ = Х^-₁₁ и z₁₁ = z^-₁₁ = 30,9.

в) Учитывая полученный результат, легко найти X⁺₁₂ = (0,15; 0,15) и z⁺₁₂ = 34,5 > z₁₁ (точка Х⁺₁₂ должна быть отброшена).

г) Величина z, вычисленная в точке Х^-₁₂ = (-0,15;-0,15), оказывается допустимой: z^-₁₂ = 27,6 < z₁₁, т. е. Х₁₂ = Х^-₁₂ и z₁₂=27,6.

Очевидно, точка X₁₂ выступает здесь в роли Х_1n (n = 2) и, следовательно, операция г) завершает первый цикл поиска X^*, z^*.

Рассмотрим отрезок, соединяющий Х₁₀ с Х₁₂, на продолжении которого находится Х₂₀. Координаты точек Х₁₀, Х₁₂, Х₂₀ связаны зависимостями (1+а)-x_j(12) = x_j(20)+ax_j(10), где а - показатель отношения, в котором точка X₁₂ делит отрезок [Х₁₀, Х₂₀]. Выбирая, например, а = 2, имеем Х₂₀ = (-0,45; -0,45) и z₂₀ = 20,8.

д) Второй цикл решения начинается с проверки точки Х⁺₂₁ = (- 0,3; - 0,45), в которой z⁺₂₁ = 21,1 > z₂₀; затем проверяется Х^-₂₁ = (- 0,6; -0,45), где z^-₂₁ = 22,8 > z₂₀, поэтому Х₂₁ = Х₂₀ (совершить переход из Х₂₀ не удалось).

е) Обращаемся к Х⁺₂₂ = (- 0,45; - 0,3) и получаем z⁺₂₂ = 23,5>z₂₀. Наконец, в точке Х⁺₂₂ = (-0,45; -0,6) появляется удовлетворительное значение z^-₂₂ = 20,4<z₂₀; таким образом, Х₂₂ = X^-₂₂ и второй цикл завершен. Построение точки Х₃₀ проводится при том же а = 2, что дает Х₃₀ = (-0,45; -0,9) и z₃₀ = 14,2. Третья и последующие конфигурации определяются так же, как первые две; в результате возникает траектория "движения" к X^*, показанная на рис. 6.9 (последний, восьмой цикл реализован при ΔX_J = 0,1); точка (1; -2,95) принимается за X^*; исследование ее окрестности подтверждает правильность найденного решения.

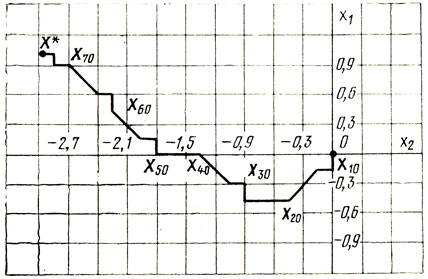
Рис. 6.9

Рассмотренные в гл. 5, 6 методы могут найти применение тогда, когда эксперименты позволяют получать точные значения z. Подобное предположение не всегда допустимо. Очень часто приходится считаться с наличием тех или иных возмущений (прежде всего - ошибок эксперимента), нарушающих запланированный ход решения задачи. Анализу вопросов, связанных с учетом этого фактора, посвящена следующая глава.