8.5. Анализ возможных ограничений. Необходимость стандартных предпосылок

Требование минимизации Т_с должно сопровождаться выполнением ряда ограничений, упоминавшихся выше. Очевидно, предсказать все возможные ограничения нельзя, поэтому обратим внимание лишь на те, которые достаточно широко распространены и часто встречаются в практических задачах.

I. Одним из наиболее существенных является предположение о характере изменения длительностей (τ_sk) выполняемых работ. Если эти длительности фиксированы, возникают задачи составления оптимальных планов (расписаний) производства работ в системе, решаемые обычно с использованием комбинаторных методов и отражающие основные трудности, с которыми сталкиваются исследователи проблем планирования. Если же допускаются вариации каждого значения τ_sk в каких-то пределах, задача достижения minT_c упрощается и сводится к назначению норм времени на технологические операции. Эти особенности позволяют различать задачи нормирования (с гладкой структурой) и задачи собственного планирования (с дискретной структурой), одинаково важные с точки зрения запросов практики, но неравноценные в методологическом отношении.

II. Весьма важным является требование непрерывности производства работ (начатая работа или ее этап выполняется без перерывов до полного завершения). Отказ от этого требования представляется своего рода компромиссом, расширяющим область возможных значений τ_sk и упрощающим процедуры решений.

III. Широко распространены ограничения, связанны- с заданием директивных сроков окончания отдельных работ. Пусть имеются Н групп, объединяющих соответственно по η_υ различных работ

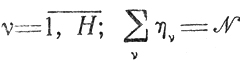
и для каждой υ-й группы задан общий срок t_g(υ) полного (т. е. по всем M этапам) завершения работ. Номера s, под которыми рассматриваемые работы проходят на k-u участке, составляют множество S_k(υ), включенное в {1, 2,. .., N}, причем S_k(υ) может быть образовано различными способами. Момент, когда υ-я группа освободит систему, найдется как

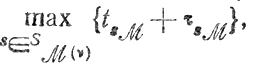
поэтому исследуемые ограничения принимают вид

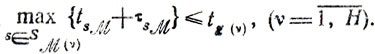
Можно попытаться выбрать надлежащим образом состав множеств

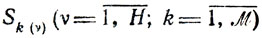
и указать тем самым допустимый порядок проведения работ. Очевидно, подобные ограничения плохо формализуются, хотя в некоторых случаях удается получить нужные соотношения. Положение не меняется, если вместо t_g(υ) заданы директивные сроки начала работ.

IV. Другой важный класс образуют ограничения приоритетного характера, позволяющие с самого начала частично упорядочить последовательность выполнения работ. В рамках принятой модели систем производственного типа можно говорить об абсолютных приоритетах, распространяющихся на все M участков (некоторые работы не разрешается делать раньше каких-то других на всех этапах), и об относительных приоритетах, устанавливаемых лишь в пределах того или иного участка. Широко применяемый на практике способ задания приоритетов сводится к следующему: назначается ряд показателей приоритетности (натуральные числа 0, 1, ....,П), присваиваемых отдельным группам работ (количество групп равно

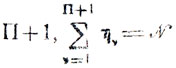
Группа с высшим приоритетом "0" принимается на обслуживание в первую очередь, группа с приоритетом "1" - во вторую очередь и т. д.; работы, входящие в одну произвольно взятую группу, не имеют преимуществ очередности друг перед другом. Последнее замечание позволяет свести многие задачи с приоритетными ограничениями к более простым задачам без этих ограничений, что особенно важно в условиях, когда возможности формализации минимальны.

V. Для большинства технологических процессов, распадающихся на этапы, характерно существование связи между моментами начала очередного k-го этапа любой работы и завершения ее (k-1)-го этапа. Если какая-то работа имеет на k-ы участке номер s(1≤s≤N), а на (k-1)-м участке - номер р (1≤p≤N) то возникает ограничение t_p,k-1+τ_p,k-1-φ_p,k-1≤t_sk, где φ_p,k-1 - время, на которое момент t_sk опережает момент t̄_p,k-1.

Неотрицательная величина φ_p,k-1 либо определяется конкретными особенностями технологии, либо выбирается произвольно из интервала

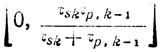
его верхняя граница получена из условия пропорциональности затрат времени

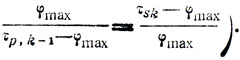
Вводить φ_p,k-1 в качестве самостоятельной переменной имеет смысл, по-видимому, только в задачи с дискретной структурой. Более широкая координация работ в системе находит свое формальное выражение в аналогичных неравенствах t_pq + τ_pq-φ_kq≤t_sk, где t_pq, t_sk - моменты начала работ с номерами pq, (q≤k-1); - координационная поправка, имеющая размерность времени.

Перечисленные выше категории ограничений слабо связаны с физической природой исследуемых систем и обладают поэтому известной степенью общности. Вместе с тем всегда можно ожидать появления и каких-то специфических требований к структуре расписаний. Например, часто допускается использование одного и того же оборудования для выполнения разных этапов работ, ставится условие прерывания производственного процесса в заранее заданные моменты времени, варьируется производительность технологических линий и т. п. Многие из таких ограничений ослабяются путем искусственного увеличения числа N, формального введения фиктивных операций, установления дополнительных приоритетов. Эти меры оказываются полезными и в случаях, когда на вход системы поступает поток заказов. Их источник может рассматриваться как своеобразная подсистема, работа которой регламентируется директивными сроками.

Сделанные замечания подтверждают необходимость стандартизации исходных предпосылок в интересах разработки единых методов планирования. Отказ от этого принципа только усложнит проблему разрешимости общей задачи теории расписаний и сузит возможности

практического использования результатов. В дальнейшем, основное внимание уделяется перечисленным выше ограничениям, обладающим известной универсальностью.