8.6. Интерпретация условий общей задачи планирования

Соотношения, полученные в § 8.4, могут быть в какой-то степени конкретизированы посредством несложных преобразований. Очевидно, формула (8.2) представляет собой разностное уравнение

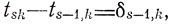
где

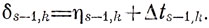
Его решение при

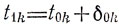
есть

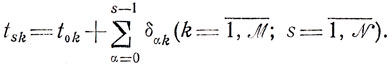(8.7)

Если подставить (8.7) в (8.1), то получаемое выражение

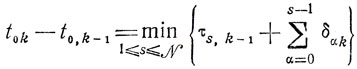
тоже является разностным уравнением, позволяющим прийти к формуле

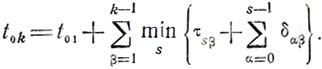(8.8)

Независимо от того, как организованы работы в масштабе всей системы, можно утверждать:

а) момент начала последней работы на k-м участке не наступит раньше момента полного завершения (k-1)-й операции, т. е.

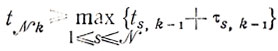
или

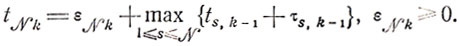
б) Момент полного завершения k-и операции совпадает с моментом окончания последней работы на k-ы участке, т. е.

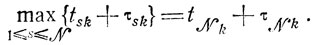
Отсюда

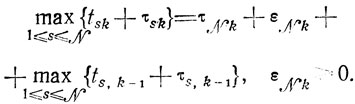
Таким образом, возникают новые соотношения

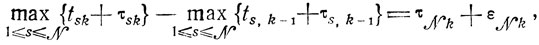
приводящие к равенству

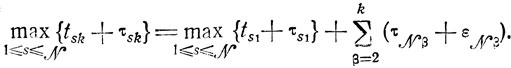(8.9)

Полагая в (8.9) k=M и используя формулы (8.6), (8.7), а также

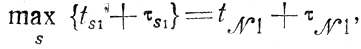
получаем развернутое выражение критерия:

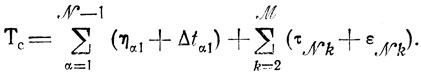(8.10)

Соотношения (8.6) - (8.9) позволяют получать и удобные формы записи ограничений; например, требование t_sk≥t_p,k-1+τ_p,k-1 (см. § 8.5) может быть представлено как

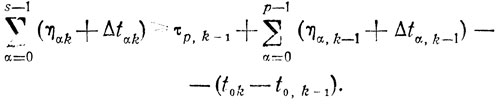(8.11)

Трудности составления расписаний для систем взаимодействующих участков при фиксированных заранее величинах t_sk связаны с отсутствием в большинстве случаев условий существования оптимума и такими внутренними свойствами моделей, которые не всегда поддаются формальному описанию,

Пусть в общую задачу планирования (см. § 8.3) введены ограничения только IV и V типов (см. § 8.5). Существует теорема (18): чтобы неравенства t_sk≥t_p,k-1+τ_p,k-1 соблюдались, необходимо и достаточно выполнить условия t_sk≥t_s,k-1+η_s,k-1 (s = 1,...,N, k = 2,..,M) независимо от того, каким образом, установлены относительные приоритеты.

Это утверждение вместе с формулами (8.10), (8.11) позволяет дать следующую формулировку задачи системного планирования: найти значения переменных η_αk, ε_Nk, τ_Nk, Δt_αk,

Доставляющие

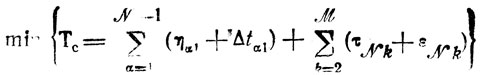
при ограниченных

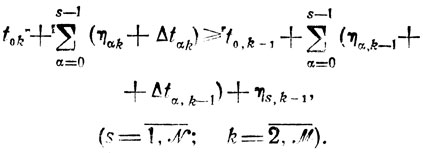
Её особенность состоит в том, что неясны допустимые значения переменных η_αk даже при известных τ_sk причём с увеличением числа ограничений трудности определения η_αk только возрастают. Таким образом, возникает задача с неполной информацией, решение которой вряд ли возможно без предварительного устранения указанной неопределенности. Это, в свою очередь, приводит к постановке вспомогательных задач различной степени сложности.

Эффективный поиск оптимальных (или близких к ним) расписаний для систем конвейерного типа станет возможным тогда, когда будет указана совокупность частных задач, удовлетворяющих двум основным требованиям их решения получаются сравнительно просто (т. е. при умеренных затратах материальных средств и машинного времени) и являются конструктивными (т. е. содержащими нужный результат); последовательность таких решений приводит к формированию системного плана с заданными показателями качества.

Реализация этого утверждения связана с разработкой принципов составления расписаний в общем случае, основанных на изучении свойств и структуры исследуемых оптимизационных задач. Указанные принципы могут затрагивать и характеристики изучаемой производственной системы, поскольку расписания не существуют сами по себе, они всегда связаны с системой и отражают ее особенности. Рекомендации, получаемые из анализа задач теории расписаний, должны оказывать влияние на такие общие показатели, как состав оборудования участков, производительность технологических линий и т. п. Таким образом, поиск формальных решений, относящихся к проблеме оптимальной организации процессов производства, становится средством машинного (автоматизированного) проектирования соответствующей системы.