Глава девятая. Принципы формирования расписаний в системах конвейерного типа. Подготовка плановых решении

9.1. Условия оптимального взаимодействия участков. Декомпозиция систем

Календарное планирование в масштабе всей системы с учетом различных ограничений требует разработки ряда принципов, позволяющих свести исходную общую задачу к нескольким сравнительно простым частным задачам. Эти принципы должны формироваться независимо от конкретных условий функционирования систем, представленных рассматриваемыми здесь моделями.

Пусть множество допустимых значений переменных исходной задачи планирования не пусто, т. е. ограничения совместны. Рассмотрим лишь те из них, которыми связаны работы с номерами "1, k-1", "N, k-1", "1, k", "N, k". Можно утверждать

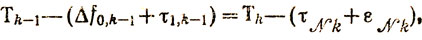(9.1)

где Т_k - полное время занятости k-го участка N работами; Δt_0,k-1 ≥з_k-1 - задержка начала выполнения работ на (k-1)-м участке при норме потерь времени з_k-1, τ_1,k-1 - продолжительность первой работы на (k-1)-м участке; τ_Nk- продолжительность N-й работы на k-м участке; ε_Nk≥0- задержка начала работы с номером "N, k" относительно момента окончания работы с номером "N, k-1" (рис. 9.1).

Время Т_с оценивается здесь как

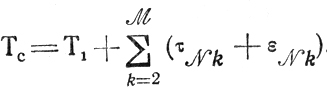
Любая из величин Т_k (k = 1,...,М) есть скалярная

функция векторного аргумента, составляющими которого являются известные длительности работ по этапам (τ_sk) и простои (Δt_s-1,k), неизбежно возникающие в каналах из-за организационных неувязок и необходимости учета всех ограничений, входящих в систему g_i(X)≤b_i.

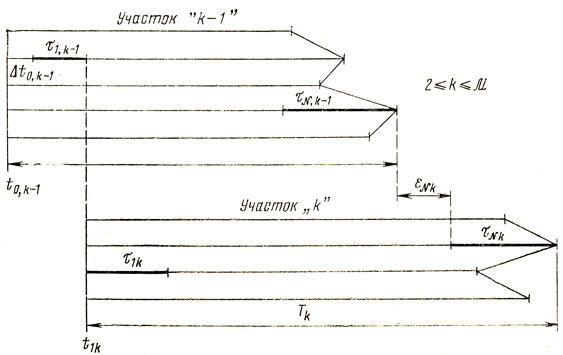
Рис. 9.1

Существуют точные нижние границы inf Т_k, и их можно было бы достичь, составляя оптимальные схемы загрузки каждого участка отдельно. В реальных условиях, когда планы участков взаимосвязаны, на результат решения задачи системного планирования начинают влиять расхождения х_k = Т_k-inf T_k и сверхнормативные потери z_k-1=Δt_0,k-1,-з_k-1. Чтобы выяснить степень этого влияния, обратимся к задаче: найти x_k, ε_Nk, z_k-1, доставляющие

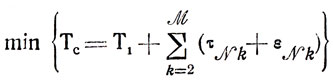
при

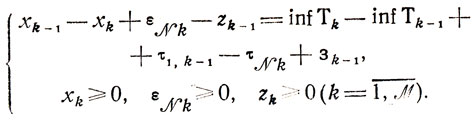(9.2)

Очевидно, равенства (9.2) являются повторением (9.1), и смысл представленной задачи (она относится к классу линейных) заключается в поиске возможностей свести решение проблемы организации взаимодействия участков к исследованию более частных задач оптимального планирования (например, к случаям М=1 или _ku = 1 и т. п.). Анализ такой промежуточной задачи линейного программирования становится целесообразным, если удается избежать громоздких процедур решения (как это имеет место в данном случае).

Из выражения Т_с следует, что всякое допустимое базисное решение системы (9.2), содержащее в числе свободных переменные x₁, ε_Nk (k = 2,...,M),будет и оптимальным. Но подобные решения могут быть получены далеко не всегда, поэтому необходимы дополнительные оценки свойств (9.2).

Теорема (19): среди оптимальных базисных решений системы (9.2) всегда найдется такое, которое содержит в числе свободных переменную х₁, все переменные z_k-1, и одновременно удовлетворяет требованиям x_kε_Nk = 0, k = 2,...,M (x_k может войти в базис только тогда, когда ε_Nk является свободной, и наоборот).

Доказательство: пусть K есть множество номеров k, таких, что ε_Nk является базисной переменной при k∈K (соответственно x_k является свободной); пусть далее k_ε есть наибольший из номеров k∈K. В этой ситуации нетрудно указать те ε_Nk которые заведомо относятся к числу свободных (они собраны под знаком

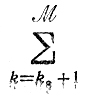
равенстве

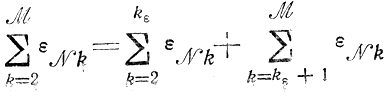
Независимо от того, какие ещё х_k, ε_Nk (k<k_ε) являются свободными, а какие базисными, можно утверждать

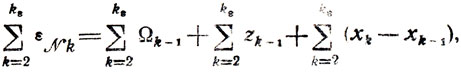
где

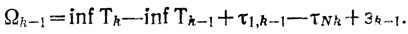
Таким образом, выражение Tc, отвечающее рассматриваемому базисному решению, имеет вид

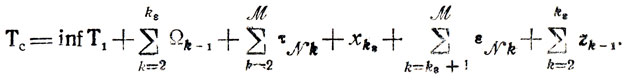
Все входящие в него свободные переменные имеют неотрицательные коэффициенты (признак оптимальности, см. п. 1.4). □

Из сказанного следует, что достижение минимума Т_c всегда обеспечивается оптимальной организацией работ на участке 1 (x₁≡0), хотя к остальным участкам подобное требование может не относиться (это зависит от величин Ω_k-1, k = 2,...,M),

Оптимальные базисные решения систем (9.2) могут иметь структуру, отличную от той, которая указана в условиях теоремы (19). Чтобы убедиться в этом, достаточно перевести в разряд свободных переменные

х_M, ε_Nk k = 2,...,M) и положить x_k-1z_k-1=0 (k = 2,...,MЖ).

Такой переход означает решение задачи планирования "в обратном времени" без изменения результатов.

Оптимальность плана первого (или последнего) участка понимается здесь условно, поскольку учесть сразу все ограничения вряд ли возможно (какие-то из них распространяются на всю систему). В дальнейшем, по мере уточнения особенностей исследуемой общей задачи, будет уточняться и рассматриваемое понятие оптимальности (окажется целесообразным связать его требованием получить наилучшую оценку нижней границы множества значений Т_c).

Предположим, что участок 1 имеет наименьшее количество технологических линий, т. е. L₁<L_k (k = 2, ...,M), и на одну линию приходится, следовательно, наибольшее число работ. В этих условиях нетрудно указать способ построения системного плана, позволяющий определить верхнюю границу расписания, превышать которую не имеет смысла: произвольно взятому каналу I участка 1 ставится в соответствие (например," по признаку совпадения номеров) один канал k-го участка (2≤k≤M) рассматривается система, объединяющая только эти l-е каналы (всего можно образовать L₁ таких систем). Если распределение работ по каналам участка 1 известно, вводится требование найти оптимальные планы проведения работ в каждой из указанных одноканальных систем с учетом исходных ограничений. В результате простого объединения этих планов возникает общий план, который не является искомым оптимальным и должен выступать лишь как предварительный.

Таким образом, удается перейти (по крайней мере на первых шагах) к анализу упрошенных задач составления расписаний, в которых легче учесть ограничения типа тех, которые упоминались в § 8.5. Основным недостатком здесь является неполная загрузка имеющихся каналов (на k-м участке остаются незанятыми L_k-L₁ линий), и это приводит к необходимости дополнительных исследований.

Предположение о том, что L₁<L_k (k = 2,...,M), не должно рассматриваться как слишком жесткое. Чтобы построить предварительный системный план при произвольном L₁, достаточно найти участок m, для которого

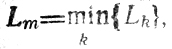
положить число каналов первого участка равным L_m и решить задачу оптимального распределения работ на нем в новых условиях. Тем самым определится и оптимальный план m-го участка; он может быть зафиксирован и использован тогда, когда возникнет необходимость возвратиться к рассмотрению первого участка со всеми L₁ каналами.

Практическое применение этого принципа связано с назначением порядка ввода в действие технологических линий, оставшихся свободными^* что представляет самостоятельную задачу.