9.3. Последовательные коррекции расписаний. Анализ сходимости процесса

Всякая перестройка расписания на отдельно взятом k-м участке может рассматриваться как некоторое "возмущение", проходящее через систему участков с номерами p>k и вызывающее ее реакцию - смещение границ значений Т_с. В общем случае нет необходимости добиваться совпадения реального Т_с с идеальным показателем Т^*_с(и), поэтому последующие оценки даны с учетом допустимой конечной погрешности δ_Д≥0, назначаемой пользователем технологической системы применительно к условиям ее функционирования.

Пусть начальная разность (погрешность) E₁ = Т̂_с(l)-Т^*_с(и), полученная в ходе формирования предварительного системного плана, уменьшается на величину ΔE₁≥0 после того, как проведены все операции, связанные с перераспределением работ на участке 2 и соответствующей переоценкой Т_с. Значение ΔE₁ = 0 допускается потому, что в отдельных случаях (например, при плотной загрузке третьего, четвертого и т. д. участков) "возмущение", возникшее на участке 2, не вызовет желаемого эффекта, и E₁ останется прежней.

Новая разность E₂ = E₁-ΔE₁ может быть уменьшена на ΔЕ₂ путем коррекции расписания на участке 3 и т. д. Суммарная поправка, накопившаяся в результате m-кратного повторения процедур улучшения планов, составит

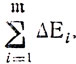
Процесс перехода от предварительного системного плана к оптимальному (квазиоптимальному) успешно завершится, если хотя бы одно из чисел конечной последовательности E₁, Е₂, ... удовлетворит условию Е_i≤δ_д при существующих отношениях Е₁≥Е₂≥.. .≥Е_m. Именно в таком смысле удобно определять здесь сходимость процесса в целом, не затрагивая пока вопроса о затратах материальных средств и времени на получение тех или иных ΔE_i (эти затраты зависят от эффективности частных алгоритмов и должны исследоваться специально).

Чтобы обеспечить сходимость в указанном смысле, достаточно иметь

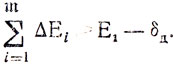(9.5)

Применительно к общей схеме "прямого и обратного времени" это неравенство принимает вид

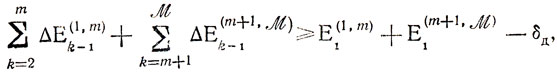(9.6)

где Е^(1,m)₁ и E^(m+1,M)₁ - погрешности предварительного планирования работы двух групп участков с номерами от 1 до m и от m до M соответственно; ΔE^(1-m)_k-1 и ΔE^(m+1,M)_k-1 - поправки от улучшения расписании участков в рассматриваемых группах.

Условия (9.6) являются довольно сильными, так как в них отражено требование ввода коррекций на всех М-1 участках. При поэтапном улучшении системного плана подобное требование иногда оказывается излишним (например, начальное рассогласование E₁-δ_д невелико и устраняется первыми же поправками). Полезность формулы (9.6) заключается в том, что она отражает идею разделения участков на группы и может использоваться в расчетах, хотя не отличается в принципе от (9.5).

Серьезную трудность представляет определение характера связей между отдельными ΔE_i и теми действиями, которые приводят к их получению. Следует признать, что сложность структуры расписаний, дискретность изменения параметров задач, большое количество вариантов плана и т. п. практически исключают возможность построения более или менее простых детерминированных моделей, позволяющих выявить эти связи. Среди вероятностных моделей, которым приходится отдавать предпочтение, наиболее приемлемыми по смысловому содержанию могут считаться модели, основанные на идеях стохастической аппроксимации, однако они требуют задания конкретных правил перехода от одной точки пространства переменных к другой, и эти правила обычно отражают существенные свойства тех же детерминированных схем. Преодолеть указанные трудности удается в какой-то мере при использовании априорных оценок вероятности выполнения условий (9.5).

Предположим, что все операции преобразования плана k-го участка дали поправку ΔE_k-1≥0, представляющую собой случайную величину с возможными значениями {ΔE_j,k-1} и рядом распределения {p_j,k-1}.

Вероятность события ΔE_k-1≥α при произвольном α>0 определяется как

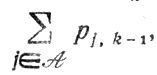
где A - множество номеров j, для которых ΔE_j,k-1≥α. Математическое ожидание ΔE_k есть

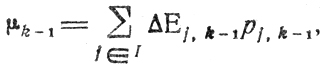
где I- множество всех j. Очевидно,

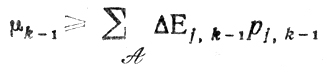
и тем более

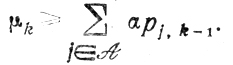
Поскольку а постоянно, последнее неравенство означает

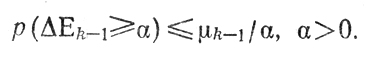(3.7)

Важность соотношения (9.7) заключается в его универсальности, но именно это обстоятельство затрудняет достижение в каждом отдельном случае высокой точности результатов.

Если α ≡ E_k-1-δ_д, то (9.7) дает верхнюю оценку вероятности успешного окончания процесса планирования после того, как улучшено расписание работы k-го участка. В дальнейшем удобнее пользоваться формулами

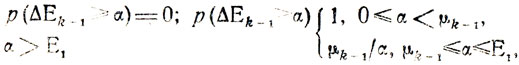(9.8)

которые полнее учитывают реальные ограничения задачи.

С помощью (9.8) нетрудно получить нижнюю оценку вероятности события, состоящего в совместном выполнении условий

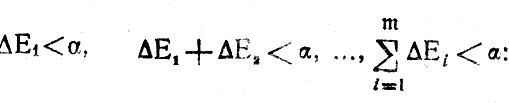
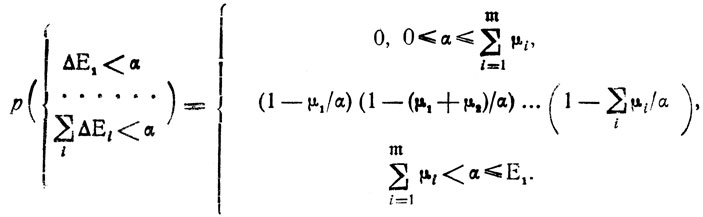(9.9)

Выражения (9.8), (9.9) позволяют перейти непосредственно к отысканию предельных вероятностей успешного формирования оптимального системного плана. Начальное рассогласование E₁-δ_Д будет устранено поочередным корректированием планов ш участков (m≤μ-1), если удастся удовлетворить хотя бы одно из требований

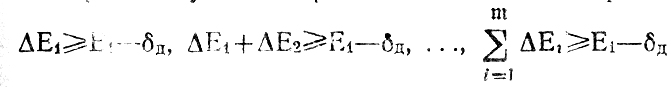
или, что то же, нарушить требование совместного существования неравенств

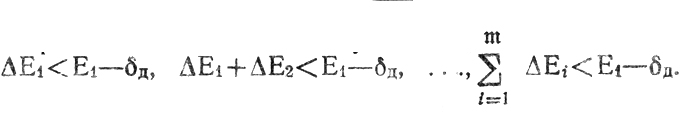
Вероятность подобного события, как это следует из (9.9), определяется математическими ожиданиями μ_i, а также величиной E₁-δ_д ≡ α. Всегда можно рассматривать μ_i, как некоторую часть от Е₁ поскольку ни одна из поправок ΔE_i не превышает E₁ (иначе нужно ставить под сомнение правильность вычисленного значения Т^*_c(и)). То же самое относится к любой из сумм и,-, входящих в правую часть (9.9); следовательно,

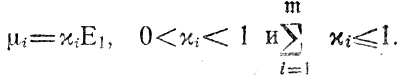
По аналогии E₁-δ_д = εE₁ при 0≤ε≤1.

Неизменность структуры расписаний, стандартизация процедур ввода коррекций, общность принятых оценок р и т. п. могут служить основанием для того, чтобы в первом приближении считать все χ₁ одинаковыми, равными χ. Это приводит к выражению

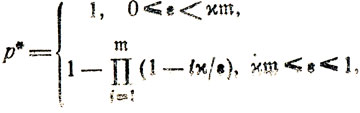(9.10)

где р^* - искомая предельная вероятность того, что условия сходимости процесса будут выполнены.

На рис. 9.4 представлены графики зависимости р^* = р^*(m), построенные для разных значений χ/ε. С увеличением m вероятность p^* только возрастает, и каждому конкретному отношению x/e = const соответствует граничное число m_гр = [ε/χ], последствия превышения которого не могут быть предсказаны априори с приемлемой точностью. Очевидно,имеет смысл корректировать расписания сначала на m_гр участках (если m_гр<M-1), а затем принимать решения (возможно, неформальные) относительно необходимости распространить этот процесс на другие участки.

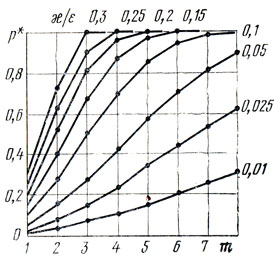
Рис. 9.4

Полученные оценки представят интерес тогда, когда будут сформулированы правила выбора нужного значения χ/ε. Поскольку величина ε определяет устраняемую часть начальной погрешности E₁ и характеризует желаемую точность конечного результата, она должна быть задана, например, пользователем системы или оператором, организующим технологический цикл. Что касается х, то в рамках гипотезы χ_i=χ удается провести необходимые вычисления, основанные на использовании формул (9.4) или соответствующих графиков (рис. 9.3) применительно к последнему, M-му участку. Здесь при известных N и L_M, отыскиваются ожидаемые T̄, появление которых обусловлено последовательным подключением L_M-L_m резервных каналов. Найденный суммарный эффект пересчитывается в отношение к E₁ и отождествляется с χ. Это допустимо по двум причинам: во-первых, формула (9.4) дает усредненные T̄, и, во-вторых, любой выигрыш во времени, получаемый на M-м участке, становится показателем улучшения расписания системы в целом. Случай m-M исключается переходом к схеме "обратного времени".

Принятая в качестве "рабочей" величина χ/ε определяет m_гр - число участков, планы которых должны обязательно корректироваться. Если это требование выполнимо (m_гp<M-1), то экономятся средства, затрачиваемые на решение задачи; если же m_гр>M-1, то возникает вопрос о приемлемости р^*<1, целесообразности изменения е и т. д; подобные ситуации нужно анализировать и после того, как коррекции введены. При неблаго

приятном исходе

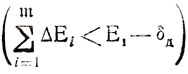
роль неформальных приемов уточнения имеющегося плана может заметно возрасти. Здесь полезно обратить внимание и на ряд других обстоятельств, подчеркивающих важность участия человека в процессе преобразований общесистемных расписаний и поиске приемлемых вариантов решений задачи.

Обращение к неформальным оценкам может быть обусловлено:

- отсутствием алгоритмического языка, который позволил бы представить и исследовать расписание в целом (подобно тому, как это делает человек, оперирующий с Гантт-картой);

- включением алгоритмов планирования в схему оперативного управления технологическим процессом, предполагающим многократное (частичное или полное) решение задач составления расписаний с выбором начала повторений применительно к складывающейся обстановке;

- необходимостью согласования различных решений (в том числе и плановых) в масштабе всей АСУ того или иного уровня.

Проведенный анализ условий сходимости процесса корректирования системных планов показал, что даже в условиях неопределенности (характерных для общей задачи составления расписаний, см. п. 8.6) можно предсказывать ожидаемые результаты планирования и давать оценки соответствующих вероятностей благоприятного исхода коррекций.