10.3. Вычислительная эффективность алгоритмов загрузки линий. Динамика роста затрат

Отдельного изучения требуют вопросы, относящиеся к определению числа перебираемых вариантов решений на разных этапах поиска Т^* и Т^*_с(и). Очевидно, построение П₀ делением суммы всех τ_j (j = 1,...,N) на L примерно равных частей (см. п. 10.1) дает разницу между

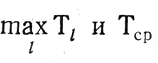
порядка

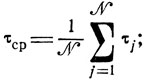
можно ожидать, что разница между

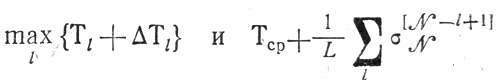
составит здесь величину, приближающуюся к

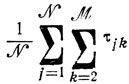
(тем более, что всегда допустимо строить П₀, ориентируясь сразу на max {Т_l+ΔT_l}). Количество элементарных операций, приводящих к получению П₀, невелико и имеет порядок N (упорядочение N чисел с одновременным составлением L сумм, оценка

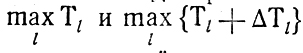
варианты предварительной загрузки линий даже не сравниваются между собой). Более подробные исследования вряд ли нужны, поскольку речь идет о начальной фазе планирования, малая трудоемкость которой не вызывает сомнений.

Если теперь обратиться к процедурам решения диофантовых уравнений, завершающим составление расписаний для рассматриваемого изолированного участка, то оценки затрат, приведенные в § 10.1, указывают на резкое возрастание числа перебираемых вариантов плана (сочетаний работ). Когда ставится цель найти все оптимальные решения, это число приближается к 2^N, однако оно может быть уменьшено приблизительно на порядок (т. е. примерно до 2^N-3) за счет тщательного отбора значений B (см. § 10.1). Существенного улучшения оценок можно ожидать в случае, когда достаточно найти хотя бы одно оптимальное решение, но и здесь количество анализируемых вариантов находится на уровне 2^N/2-2^M-3.

Значительные различия трудоемкостей начальной и заключительной фаз планирования на участке приводят к необходимости более подробного изучения промежуточных состояний плана с целью уточнить характер соотношений между качеством (точностью) получаемых результатов и производимыми затратами. Пусть на очередном шаге требуется провести обмен предварительно упорядоченными работами между двумя каналами с тем, чтобы уменьшить разность Δ времен их занятости. Число работ в первом канале равно n₁, во втором - n₂. Значения τ_υ(1)(υ = 1, ...., n₁), τ_υ2(υ = 1,...,n₂) известны, причем t̄_υ(2)-t̄_υ(1)>Δ и τ₁₍₂₎>Δ для всех пар номеров υ₍₁₎, υ₍₂₎, которым отвечает условие t̄_υ(2)>t̄_υ(1) (в противном случае правила обмена станут очевидными). Наилучшим результатом здесь, как обычно, явилось бы равенство T₁+Δ/2 = T₂-Δ/2, но его достижение необязательно, поскольку имеется в виду лишь улучшение показателя max{Т₁, Т₂} (рис. 10.7,а).

Рассмотрим ряд перестановок работ в канале 2, сводящихся к замене отрезка τ₁₍₂₎ последовательно отрезками τ₂₍₂₎, τ₃₍₂₎, ..., τ_n2(2) (см. рис; 10.7,6) с соответствующими сдвигами точек t̄_υ(2). Всего таких перестановок будет n₂-1, и их использование приведет к изменению первоначальных разностей t̄_υ(2)-t̄_υ(1) и к увеличению возможности уменьшить Δ (например, в схеме, показанной на рис. 10.7,а, оказывается достаточным заменить τ₁₍₁₎ + τ₂₍₁₎ на τ_n2(2)). Формально рассматриваемая операция сводится к вычислению τ_υ+1(2)-τ_υ(2) (υ = 1, ..., n₂-1) и сравнению чисел

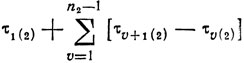
с τ₁₍₁₎, τ₁₍₁₎+τ₂₍₁₎, ... Подобные действия можно повторять, связывая их с произвольными τ_υ(2) (а не только с τ₁₍₂₎), выбираемыми на основе предварительного анализа исходных разностей t̄_υ(2)-t̄_υ(1). Схемы размещения отрезков вблизи некоторого τ_υ(2) показаны на рис. 10.7,в; первая из них строится по принципу схемы б), вторая использует обратную последовательность работ с сохранением первоначальной нумерации (рис. 10.7,а); возможности реализации этих схем расширяются с увеличением n₂. Ожидаемый результат сравнения получаемых таким образом новых t̄_υ(2) с имеющимися t̄_υ(1) - приближение max{T₁, Т₂} к 0,5(T₁+T₂) с погрешностью порядка

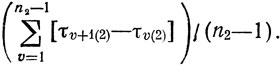
Количество сравнений (или исследуемых вариантов расстановки работ) составит 2(n₂-1)V, где V - число отрезков τ_υ(2), относительно которых проводятся все рассмотренные операции (рис. 10.7,в). Даже допуская V∼n₂/2, можно утверждать, что уровень затрат характеризуется здесь величиной порядка n²₂.

Если теперь повторить предложенную процедуру для каких-то τ_υ(1), то указанная выше погрешность будет оцениваться как

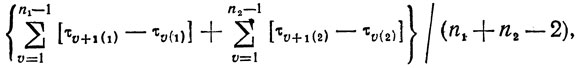
но затраты возрастут примерно до уровня (n²₁ + n²₂). По скольку всегда числа n₁ и n₂ находятся в пределах [N/L] и количество пар каналов, участвующих в обменах работами, есть C_2L∼L²/2, характер отношений между точностью результатов улучшений плана участка в целом и произведенными затратами представляется следующим: специально организованный перебор вариантов загрузки линий, сопровождаемый несложными вычислениями, позволяет достичь оптимума с погрешностью порядка

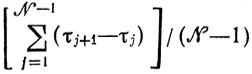
(средняя разность длительностей соседних работ в их исходной последовательности, упорядоченной по признаку возрастания τ_j, j = 1,...,N

Очевидно,

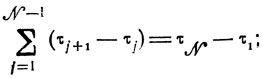
величина τ_N сравнима с τ₁ по модулю Н_τ = НОД_τj (т. е. τ_N=τ₁+k_NH_τ, k_N - целочисленный неотрицательный коэффициент), поэтому полученная оценка точности приводится к k_NH_τ/(N-1). Вырожденный случай k_N=0 (все τ_j одинаковы) мало интересен (для него решения находятся с помощью более простых схем), и в дальнейшем принимается k_N >0.

Рассмотренная процедура и связанные с ней оценки сохранятся в принципе неизменными и в случаях, когда в качестве Δ выступает (Т₂+ΔТ₂) - (T₁+ΔT₁). Здесь меняется лишь признак упорядочения работ, и вместо χ_NH_Σ, вводится произведение где H_Σ = НОД

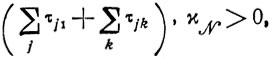
хотя в основе улучшения показателя max {(Т₁ + ΔТ₁), (Т₂ + ΔТ₂)} лежит, как и раньше, межканальный обмен работами. Усложнение вычислений выразится прежде всего в увеличении требуемых объемов памяти ЭВМ для производства тех же переборов.

Сделанные замечания позволяют составить табл. 10.1., в которой отражена динамика роста затрат при переходах от начального варианта плана к промежуточным и оптимальным.

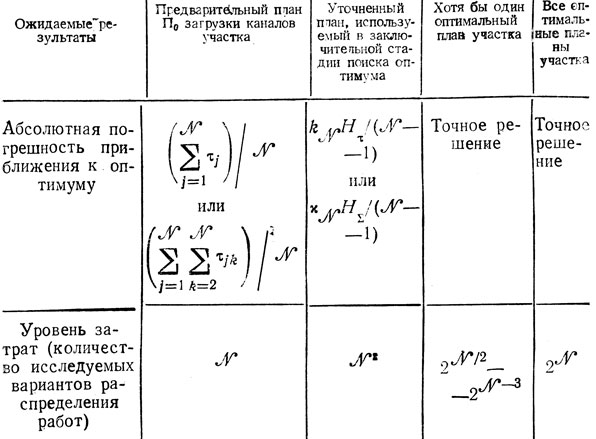
Таблица 10.1

Данные табл. 10.1 позволяют обоснованно выбирать значения ε, от которых зависит выполнение условий сходимости процесса коррекций общесистемного плана на более поздних стадиях его формирования (см. п. 9.3). Для этого нужно обратиться к анализу относительных ошибок

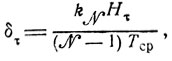
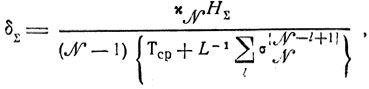
возникающих при умеренных затратах времени и материальных средств.

Имея в виду равенства Т_ср = Nτ_Ср/L, τ_cp/H_τ = k_cp (средняя продолжительность работ, выраженная в единицах H_τ) и

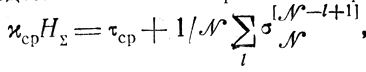
получаем

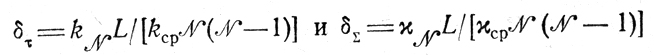
при k_N, k_cp, χ_N, χ_ср не меньших 1.

Коэффициент k_ср может быть определен как (τ₁ + τ_N)/2H_τ, поэтому k_N/k_cp≤2, ив дальнейшем имеет смысл

ориентироваться на худший случай k_N = 2k_cp.

То же справедливо и для χ_ср, следовательно, в качестве общей формулы остается

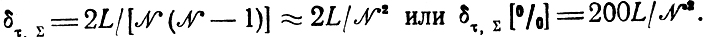(10.4)

Соотношение (10.4), характеризующее качество плана, составленного путем перебора порядка N² вариантов, оказывается полезным тогда, когда N заметно больше L, и схемы, приведенные на рис. 10.7, реальны. Это условие выполняется практически всегда, причем высокая точность приближения к оптимуму обеспечивается в широком диапазоне значений N, L.

Например, δ_τ,Σ [%] ≤ 1%, если N≥√200L (для L = 2 нужно иметь N≥20, для L = 3, N≥25 и т. д.).

Возвращаясь к е (§ 9.3), заметим, что правило его выбора принимает теперь вид

Таким образом, составление расписаний работы первого участка по предложенным схемам позволяет указать нижнюю границу множества {Т_c} и создает предпосылки для перехода к анализу задач оптимального планирования в одноканальных системах.