10.4. Планирование многоэтапных работ. Пошаговый процесс упорядочения

Рассматриваемая здесь задача представляет собой обобщение известной задачи Джонсона (см. § 8.3) на случай произвольного M>2. Ее решение в рамках общего алгоритма системного планирования (см. п. 9.5) позволяет не только улучшать промежуточные значения Т_с, но и указывать те l-системы, для которых нет необходимости составлять точное расписание.

Дана система, объединяющая M одноканальных участков, каждый из которых реализует вполне определенный этап технологического процесса. Имеются N работ, выполняемых в некоторой последовательности, и известны нормы времени τ_υk (v - номер работы по порядку следования, k - номер участка или этапа). Введены ограничения:

а) очередность работ сохраняется на всех участках неизменной (допустимость такого предположения обусловлена здесь тем, что оно упрощает исследования и затем постепенно исключается в ходе преобразования общесистемного плана);

б) момент начала k-го этапа v-й работы не может наступить раньше момента окончания ее (k-1)-го этапа;

в) для отдельных работ установлены плановые сроки скончания, которые необходимо выдержать;

г) возможна частичная упорядоченность работ (некоторые из них не должны проводиться раньше каких-то Других).

В этих условиях требуется найти последовательность работ, наилучшую в смысле минимума полного времени (Т_с(l)), затрачиваемого на их выполнение (рис. 10.8).

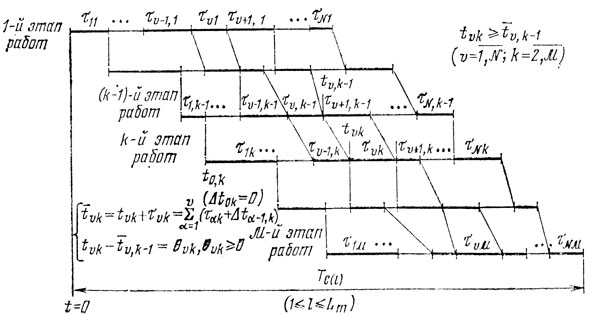
Рис. 10.8

Перечисленные ограничения не противоречат тому, что обсуждалось в § 8.5, и даны для конкретизации общих замечаний применительно к частной задаче.

Введем единый отсчет времени (t = 0); пусть t_0k - момент возможного начала k-го этапа, a Δt_υ-1,k задержка начала k-то этапа v-и работы относительно момента окончания того же этапа (v-1) работы. Очевидно, Δt_υ-1,k≥0 и условие б) может быть выражено как

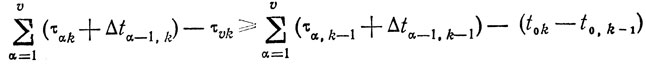
или

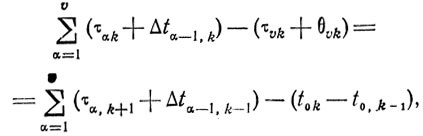(10.5)

где θ_υk - вспомогательные неотрицательные переменные (θ_υk≥0), имеющие размерность времени; Δt_0,k-1 - задержка начала (k-1)-го этапа (своего рода начальные условия).

Последнее равенство показывает, что v-я (по порядку) работа будет выполнена за время

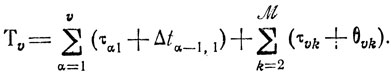
Объединив номера v, для которых существуют плановые сроки, в множество S_П, получаем формальное выражение условия в):

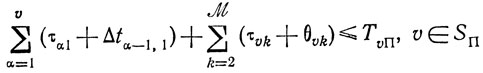
или

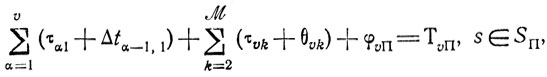(10.6)

где φ_υΠ - вспомогательные неотрицательные переменные.

Условия а) и г) связывают порядковые номера, которые получают работы, проводимые в оптимальной последовательности, поэтому формализация этих условий априори ничего не дает.

Система уравнений (10.5) может быть представлена в виде

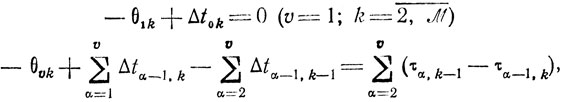
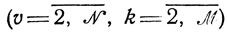
или (после попарного вычитания строк)

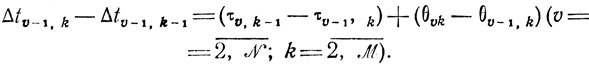(10.7)

Заметим, что всегда можно положить Δt_0k(k = 1, ..., M) равными нулю (или, что то же, включить их условно в τ_1k). Кроме того, работы подготовительные, регламентные и т. п. могут быть учтены наравне со всеми другими работами в общих соотношениях вида (10.5) - (10.7).

Обозначим

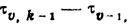
к через

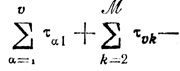
через

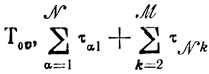
через Т₀ и обратимся к оптимизациоцной задаче: найти θ_υk, Δt_υ-1,k, φ_υΠ, доставляющие

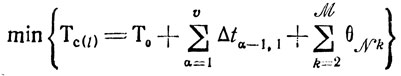
при ограничениях

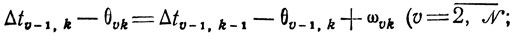
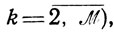
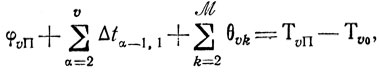(10.8)

Зафиксировав произвольным образом все τ_υk, рассмотрим эту задачу как обычную задачу линейного программирования. Из выражения Т_С(i) следует, что всякое допустимое базисное решение системы (10.8), содержащее в числе свободных переменные Δt_υ-1,1 (υ = 2, ...,N), θ_Nk (k = 2,....,M) будет оптимальным для сформулированной задачи. Однако подобные решения могут встретиться далеко не всегда, поэтому необходимы дополнительные исследования.

Обратимся к теореме (22): оптимальным является такое допустимое базисное решение (10.8), которое содержит в числе свободных все Δt_υ-1,1 и одновременно удовлетворяет требованиям Δt_υ-1,1θ_υk (υ = 2,..., N, k = 2,...,M) (переменная θ_υk может войти в базис только тогда, когда Δt_υ-1,k является свободной и наоборот).

Доказательство этой теоремы основано на последовательном отделении заведомо свободных переменных θ_υk (см. § 9.1). Чтобы найти оптимальные решения в каждом конкретном случае, достаточно использовать простое правило: если в очередной строке (10.8) сумма Δt_υ-1,k-1-θ_υ-1,k+ω_υk неотрицательна, то в базис вводится Δt_υ-1,k-1 a θ_υk считается свободной (равной нулю).Если же Δt_υ-1,k-1-θ_υ-1,k+ω_υk<0 базисной переменной становится θ_υk, a Δt_υ-1,k обращается в нуль. Сформированное решение должно удовлетворять требованиям φ_υΠ≥0(υ∈S_Π), иначе оно окажется недопустимым.

В этих условиях можно говорить об оптимальной организации работ даже при фиксированном порядке их производства (не нарушающем ограничений а)-г)). Так, этапы работы, выполняемой первой, должны следовать друг за другом без задержек (θ_1k = 0, k = 2,...,M); этапы любой промежуточной работы идут, вообще говоря, со сдвигами во времени один относительно другого (исключение составляет случай, когда все

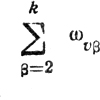
(υ = 2, ..., N, k = 2,...,M) неотрицательны).

Полученные результаты неконструктивны (они отвечают предположению τ_υk = const и не дают рекомендаций по выбору наилучшего плана проведения работ), однако появляется возможность отождествить произвольную перестановку столбцов матрицы ||τ_υk| с некоторым показателем, вычисляемым довольно просто, что должно облегчить применение здесь метода динамического программирования (или методов, сходных с ним по идее). Условия для этого следующие:

- рассматривается Пошаговый процесс планирования;

- содержанием очередного шага является размещение того или иного столбца на определенной позиции;

- перед началом очередного шага возможны только N состояний процесса, причем параметр состояния скалярный (номер столбца).

Рассмотрим теперь время Т_с(l) как функцию только τ_υk (υ = 1,...,N, k = 1, ..., M), имея в виду найденные решения. Оценка Т_С(l), получаемая при использовании рекомендаций приведенной выше теоремы и обозначаемая как T̂_C(l), обладает рядом особенностей: в общем случае Т̂_С(l) представляет собой линейную комбинацию величин τ_υk т. е.

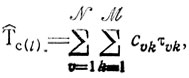
где c_φk - целочисленные коэффициенты; каждое значение T̂_C(l) отвечает заданному порядку работ, который в силу условия а) определяется порядком проведения их первого этапа (т. е. принятыми τ_υ-1 υ = 1,...,N), следовательно, τ_υk есть однозначно определенная функция τ_υ1 (υ = 1,...,N),

Учитывая эти замечания, получаем

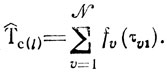
Возможные наборы значений τ_υ1 образуются при перестановках N элементов первой строки матрицы ||τ_υk||, и множество всех таких перестановок объединяет N! элементов. Наиболее удобным для практической реализации представляется метод поиска оптимума Т̂_С(l) по переменным τ_υ1 основанный на идее непосредственного пошагового формирования искомой расстановки работ и сводящийся к анализу промежуточных состояний и наилучших продолжений процесса планирования. Исходными данными здесь являются конкретизированные ограничения в), г) и матрица ||τ_υk|| с фиксированной произвольным образом нумерацией столбцов (исходная нумерация работ).

Основные этапы решения задачи: вводится предположение о том, что (N-1)-ю позицию занимает первая (по исходной нумерации) работа, и в рамках этого предположения исследуются варианты формирования двух последних позиций будущего плана ("первая и вторая работы", "первая и третья работы", ..., "первая и N-я работы"); для каждого такого варианта определяются

ω_υk=τ_υ,k-1-τ_υ-1,k, Δt_υ-1,k, θ_υk при υ = N, k = 2,..,M, проверяется выполнение условий в), г) и оцениваются величины

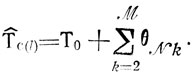
При проверках в) используются приближенные оптимистические показатели, вычисляемые для идеализированного случая, когда все θ_υk, Δt_υ-1,k(υ = 2, ....,N-1; k = 2,...,M) положены равными нулю. По мере накопления информации достоверность этих показателей растет, и в конечном счете они переходят в T̂_c(l)υ.

Вводится предположение о том, что (N-1)-ю позицию занимает вторая (по исходной нумерации) работа, и в рамках этого предположения исследуются варианты формирования двух последних позиций плана ("вторая и первая работы", "вторая и третья работы", .."вторая и N-я работы"). Для каждого варианта отыскиваются ω_υk, θ_υk, Δt_υ-1,k(υ = N; k = 2, ...,M), проверяются условия в), г) и оценивается Т̭_с(l).

Рассмотренные операции повторяются для оставшихся предположений, связанных с размещением третьей, четвертой, ..., N-и работы на (N-1)-й позиции. Таким образом, оказываются исследованными ,N(N-1) вариантов, и становится возможным их сравнение с целью

указать наилучшие из полученных Т̂_С(l) (все это удобно свести в первую таблицу результатов, содержащую перечни вариантов, допустимых по ограничениям а)-г) и упорядоченных по признаку ухудшения Т̂_С(l)).

Вводится предположение о том, что (N-2)-ю позицию занимает первая (по исходной нумерации) работа; 3 рамках этого предположения исследуются варианты формирования трех последних позиций будущего плана, причем (N-1)-я и N-я позиции (т. е. продолжение процесса) выбираются здесь как единое целое на основе использования данных первой таблицы результатов. Определяются Δt_υ-1,k, θ_υk (υ = N; k = 2,...,M), проверяются условия в), г) (по оптимистическим показателям) и оцениваются новые величины

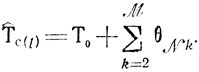
Все эти операции повторяются применительно к предположениям, связанным с размещением второй, третьей, ..N-й работ на (N-2)-й позиции, так что общее число анализируемых вариантов составляет по-прежнему N(N-1). Все результаты, не нарушающие ограничений а) -г), сводятся во вторую таблицу.

Вводится предположение о том, что (N-3)-ю позицию занимает первая (по исходной нумерации) работа, и исследуются варианты формирования четырех последних позиций будущего плана. Набор работ, попадающих на (N-2)-ю, (N-1)-ю, N-ю позиции, дает вторая таблица результатов; проводятся стандартные проверки

условий в), г), вычисляются Т̂_c(l), и, наконец, составляется третья таблица результатов; переход к новым предположениям продолжается до тех пор, пока не будут составлены и оценены последовательности из N работ.

Общее количество исследуемых вариантов в рассмотренной схеме не превысит N³ вместо N! при полном переборе (реальный выигрыш получается при N>5).

Методы составления расписаний, рассмотренные в § 10.1, 10.2, 10.4, реализуемы в сравнительно несложных программах для ЭВМ и во многом определяют исход решения общей задачи планирования (см. § 9.5). Формирование схем загрузки отдельно взятого участка и одноканальных l-систем делает возможным поэтапное улучшение общего плана на основе межканального обмена работами.