10.5. Улучшение показателей формируемых расписаний. Межканальный обмен работами

Предлагаемые здесь алгоритмы основаны на структурных преобразованиях схем предварительного распределения работ, дающих определенную информацию о достигнутых и ожидаемых состояниях формируемого плана. Последнее обстоятельство способствует упрощению процедур перестройки расписаний, хотя не исключает всех трудностей, характерных для задач упорядочения работ.

Предположим, что все подготовительные операции, связанные с построением L_m планов одноканальных систем, переходом к схеме "прямого и обратного времени", определением ε, χ/ε, m и т. д., завершены. Ситуация, возникающая на произвольном k-м участке, характеризуется в этих условиях следующим.

Моменты начала работ в каждом канале (t_0lk) не совпадают, вообще говоря, друг с другом (см. рис. 9.2), поскольку они зависят от параметров оптимальных (или квазиоптимальных) планов l-систем, формировавшихся самостоятельно.

Левый сдвиг работ в пределах любого канала невозможен (в противном случае следовало бы возвратиться к анализу планов соответствующих l-систем).

Каждой работе с номером υlk приписаны три показателя: τ_υlk (продолжительность выполнения), Δt_υ-1,lk (время простоя канала перед началом этой работы), θ_υlk (допустимый, но пока невозможный сдвиг влево), причем Δt_υ-1,lk×θ_υlk = 0.

Имеется резерв из L_k-L_m каналов, образовавшийся вследствие искусственного уменьшения L_k на начальных стадиях исследований (см. гл. 9).

Все L_m занятых каналов различаются по степени их влияния на общий результат Т_с, и это должно учитываться при перестройках расписаний. В формальных оценках допустимо считать наиболее важным в указанном смысле первый канал, вторым по важности - второй канал и т. д. (для этого достаточно изменить нумерацию), причем в ходе коррекций такое согласование номеров приходится проводить неоднократно.

Таким образом, улучшение плана k-ro участка, выражающееся в уменьшении каких-то θ_υlk>0 и соответствующих изменениях общего показателя Т_с, может быть достигнуто, во-первых, за счет межканального обмена работами и, во-вторых, за счет ввода в действие резервных линий. В первую очередь необходимо исследовать процесс обмена.

Обратимся к задаче: дан план участка в виде Гантт-карты или в виде блочной матрицы, элементами которой являются наборы чисел t_0l, Δt_υ-1,k, τ_υl, θ_υl(индекс "к" можно пока опустить). Правые сдвиги работ безусловно запрещены (этим устраняется опасность нарушения сроков T_υΠ и других ограничений, см. § 10.4, 8.5). Требуется получить условия переноса произвольно взятой работы из одного канала в другой и построить на этой основе алгоритм обмена, приводящий к наибольшему эффекту (в смысле уменьшения Т_с) при фиксированном количестве переборов.

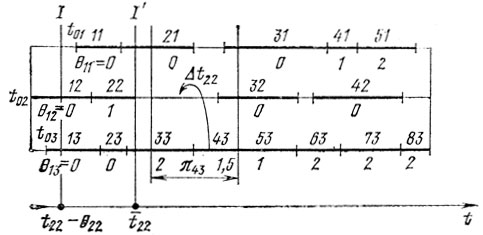
Рис. 10.9

Идею поиска вариантов обмена удобно рассмотреть сначала на частном примере. Пусть имеется схема загрузки участка с L_m = 3 и конкретными θ_υl(υ = 1, ..., n_l; l = 1,.., 3) (рис. 10.9). Нетрудно найти границы возможных левых сдвигов работ с θ_υl>0, и первой такой границей будет I (она принадлежит работе "22" с θ₂₂ = 1). Имея в виду отказ от правых сдвигов, приходим к выводу: работа "22" могла бы переходить из канала в канал, оставаясь обязательно в пределах полосы шириной t̄₂₂-t₂₂+θ₂₂, однако это невозможно из-за отсутствия в указанных пределах хотя бы одного промежутка Δt_υ-1,l≥τ₂₂. Та же ситуация повторяется для работы "33", но работа "43" оказывается в лучшем положении, так как в связанной с ней полосе π₄₃ есть Δt₂₂>τ₄₃ (рис. 10.9). Передав "43" в канал l = 2 и сместив влево работы "53"-"83", получаем новый план, после чего следует пересчет Т_с.

Формализация подобной процедуры связана с анализом схемы, представленной на рис. 10.10. Некоторая работа, принадлежащая каналу λ(1≤λ≤L_m), имеющая порядковый номер со и продолжительность τ_ωλ переводится в канал l(1≤l≤L_m, l≠λ). Левая граница полосы перемещений, отсчитанная от момента t_0l вычисляется по формуле

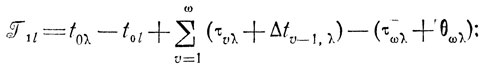
правая граница есть J_2l = J_1l + τ_ωλ + θ_ωλ. Вводя в рассмотрение единичную ступенчатую функцию 1 (t) = 0 при t<0 и 1(t) = 1 при t≥0, а также функцию F_l(t) (принимающую в произвольный момент времени t≥t_0l значение 0, если в этот момент канал l простаивает, и значение v, если в нем выполняется работа с номером υ≥1), приходим к группе условий, лежащих в основе алгоритма межканального обмена.

Теорема (23): для того чтобы оказался возможным перевод работы "ωλ" в канал l, необходимо и достаточно найти такое значение t_ωλ из диапазона; J_1l≤t_ωλ≤J_1l+θ_ωλ при котором произведение F_l(t)1[-t²+(2t_ωλ+τ_ωλ)t-t_ωλ(t_ωλ+τ_ωλ)] тождественно равно нулю.

Доказательство: поскольку для всех t<t_ωλ и t > t_ωλ+τ_ωλ значение 1 есть нуль (при этих t аргумент 1 отрицателен), имеет смысл рассмотреть случай t_ωλ≤t≤t_ωλ+τ_ωλ. Здесь 1 = 1, и выполнение условий теоремы связывается с равенством F_l(t) = 0. Пусть при не котором допустимом t_ωλ перевод работы ωλ оказался возможным, следовательно, в течение времени τ_ωλ, начиная с момента t_ωλ канал I оставался бы незанятым. Но это означает F^l(t) = 0, t_ωλ≤t≤t_ωλ+τ_ωλ (необходимость). Наоборот, если F_l(t) = 0 при t_ωλ≤t≤t_ωλ+τ_ωλ и J_1l≤t_ωλ≤J_1l+θ_ωλ то существует такое время простоя l-го канала в пределах полосы перемещений работы "ωλ", что его можно использовать для выполнения этой работы (достаточность). □

Машинная реализация рассмотренных требований сводится к анализу систем неравенств вида

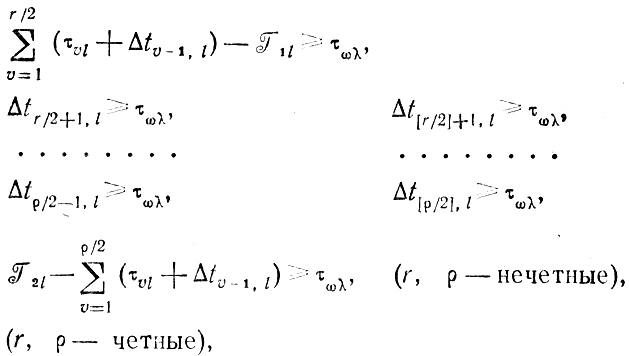(10.9)

где r и ρ - наименьшие порядковые номера сумм τ_1l, τ_1l+Δt_l1, τ_1l+Δt_1l+τ_2l, τ_1l+Δt_1l+τ_2l+Δt_2l,... превышающих соответственно J_1l, J_2l. Соблюдение хотя бы одной группы неравенств (10.9) равносильно отысканию нужного промежутка Δt_υ-1,k≥τωλ в который попадает работа ωλ.

Если операция однократного обмена между каналами λ и l проведена, фиксируются новые значения θ_ωλ, и т. п., после чего дается оценка изменений общего показателя T_c. Число исследуемых вариантов, определяющее уровень затрат на первом этапе улучшения общесистемного плана, имеет порядок NLm≤NLM (на каждом из m участков проверяются N работ с целью найти какой-либо из L каналов, допускающий разовый обмен). Реальные затраты будут скорее всего нижеуказанных здесь, так как рассматриваемым операциям предшествует уплотнение расписаний и, кроме того, присутствие различных ограничений затрудняет подбор комбинаций перемещаемых работ.