Глава 2. Элементы выпуклого анализа

2.1. Евклидово пространство. Выпуклые множества

Мы будем иметь дело с функциями, определенными на множествах конечномерного евклидова^* пространства E_n.

^* (Подробные сведения о евклидовом пространстве, как линейном пространстве с фиксированным в нем скалярным произведением, читатель найдет, например, в [10] (гл. III, § 4).)

Совокупность всех точек (векторов) x^T = (x₁, x₂, ..., x_n) с n вещественными координатами x₁, x₂, ..., x_n называют евклидовым пространством размерности n, если выполняются следующие условия. Пусть x∈E_n, y∈E_n и α - вещественное число; тогда

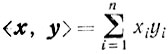(скалярное произведение).

В евклидовом пространстве введено понятие евклидовой нормы (длины вектора)

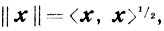
для которой справедливы следующие соотношения:

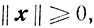
причем 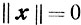тогда и только тогда, когда x = 0;

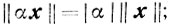
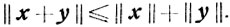
Евклидова норма и скалярное произведение связаны между собой неравенством Коши - Буняковского:

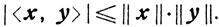
Евклидова норма порождает в E_n сходимость. Будем говорить, что последовательность {x_k} точек из E_n сходится к точке x при m→∞, то есть 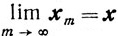, если

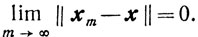
Приведем еще несколько определений. Множество

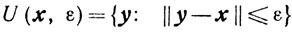
будем называть ε-окрестностью точки x.

Множество X⊂E_n называют замкнутым, если оно содержит все свои предельные точки, то есть такие точки, что любой окрестности каждой из них принадлежит бесконечно много точек из X.

Точка x∈X называется внутренней точкой множества X, если существует такая ее окрестность, все точки которой принадлежат множеству X.

Точка x∈X называется граничной точкой множества X, если любая ее окрестность содержит как точки, принадлежащие множеству X, так и точки, не принадлежащие этому множеству. Множество, состоящее из всех граничных точек множества X, называется границей множества X.

Множество X n-мерного евклидова пространства E_n называется выпуклым, если вместе с любыми двумя точками x∈X и y∈X ему принадлежит и соединяющий их отрезок [x, y].

Выпуклость множества X означает, что из x, y ∈Х следует z = αx + (1-α)y ∈X для всех 0≤α≤1. Например, в E₂ выпуклы отрезок, полупрямая, прямая, круг, треугольник, полуплоскость и вся плоскость.

Легко видеть, что если множество X задается системой линейных равенств и неравенств:

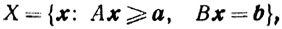
А, В - матрицы, то оно выпукло и замкнуто (последнее ввиду линейности и, следовательно, непрерывности преобразований А и В).