2.2. Проекция точки на множество. Свойства
Определение.Проекцией точки v на выпуклое множество X называют такую точку p = p(v) множества X, что
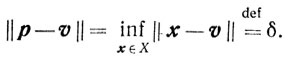 (2.1)
(2.1)При этом δ называется расстоянием точки v до множества X.
Теорема 2.1.Для любого выпуклого замкнутого множества X и любой точки v существует единственная точка p∈X, являющаяся проекцией v на X.
Доказательство. Если v∈X, то очевидно, что p = v и δ = 0. Пусть точка v - внешняя относительно X: v∉X. Согласно определению нижней грани существует последовательность {xk}, xk∈X, такая, что
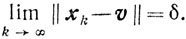
Так как {xk} ограничена, то существует подпоследовательность {xki} такая, что
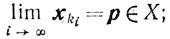
следовательно,
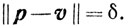
Для доказательства единственности предположим, что существуют точки p'∈X и p"∈X, p'≠р" такие, что
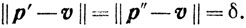
Поскольку множество X выпукло, то точка z = 1/2(p'+p") принадлежит X; но из теоремы Пифагора следует
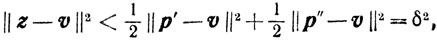
что противоречит определению δ.
Теорема 2.2.Для того чтобы точка p∈X была проекцией точки v на выпуклое замкнутое множество X, необходимо и достаточно, чтобы для всех x∈X выполнялось неравенство
<x - p, v - p>≤0.(2.2)
Доказательство. Пусть p - проекция точки v на X. Возьмем произвольную точку x∈X и рассмотрим z = αx + (1-α)р. Ввиду выпуклости X для любого α∈[0, 1] точка z принадлежит X. Так как
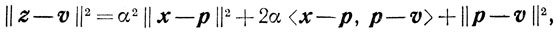
а
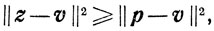
то
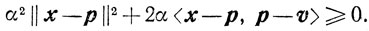
И поскольку это неравенство справедливо для всех α∈[0, 1], то
<x - p, v - p>≥0.
откуда следует (2.2),
Пусть теперь справедливо (2.2). Тогда для любого x∈X будет
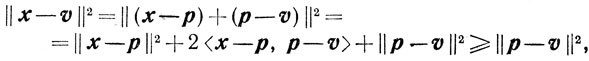
то есть p является проекцией v на X.
Следствие 2.2.Для любого x∈X
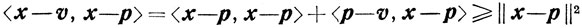
и
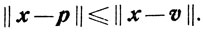
Это вытекает из того, что
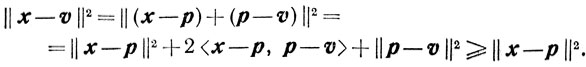
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'