2.3. Теоремы отделимости
Гиперплоскостью в En называют множество вида
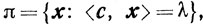
где c≠0. В пространстве En гиперплоскость определяет два полупространства:
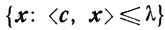
и 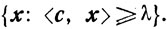
Теорема 2.3.Если X - выпуклое множество в En, то для любой точки v, внешней относительно замыкания X множества X, существует такая гиперплоскость 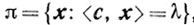 что
что
<с, v> = λ(2.3)
и для всех x∈X
<с, x><λ.(2.4)
Доказательство. Пусть p есть проекция точки v на X. Рассмотрим гиперплоскость
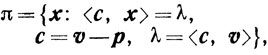
для которой выполняется (2.3). Из неравенства (2.2) следует
<x, v - p>≤<p, v - p><<v, v - p>, (x∈X).
Правое неравенство следует из (2.1) и из того, что δ>0. И, окончательно,
<с, x> = <v - p, x><<v - p, v> = <c, v> = λ,
то есть (2.4).
Замечание. Очевиден геометрический смысл теоремы: существует проходящая через точку v гиперплоскость π такая, что X лежит в одном из полупространств, определяемых π (рис. 2.1).
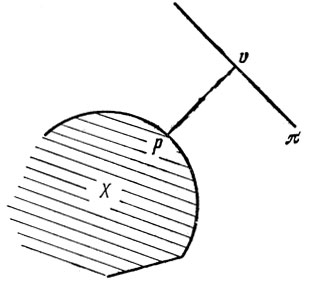
Рис. 2.1
Теорема 2.4. В любой граничной точке x0 выпуклого множества X существует опорная гиперплоскость, то есть существуют c≠0 и λ, такие, что 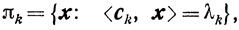
Х = <с, х0>(2.5)
и для всех x∈X
<с, x>≤λ.(2.6)
Доказательство. Рассмотрим последовательность точек {vk}, внешних относительно 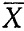 - замыкания X - и таких, что
- замыкания X - и таких, что
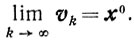
По теореме 2.3 для каждой vk существуют
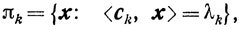
где λk = <ck, vk> и <ck, x> <λk для всех x∈X. Не умаляя общности; можно полагать ||ck|| = 1. Не меняя обозначений, будем считать, что
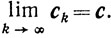
Переходя к пределу в соотношениях, определяющих πk, получим
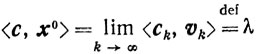
и <с, x>≤λ для всех x∈X.
Итак, гиперплоскость 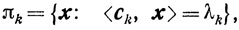 - опорная.
- опорная.
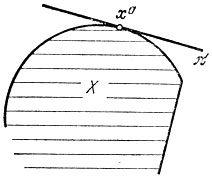
Рис. 2.2
Замечание. Легко убедиться, что если в точке х0 существует касательная гиперплоскость, то она совпадает с опорной (рис. 2.2) и в этом случае опорная гиперплоскость единственна. Однако понятие опорной гиперплоскости значительно шире понятия касательной гиперплоскости. На рис. 2.3 изображен случай, когда в точке х0 не существует касательной и в то же время в ней существуют опорные прямые, причем в качестве вектора с здесь может быть выбран любой, лежащий "между" c1 и c2.
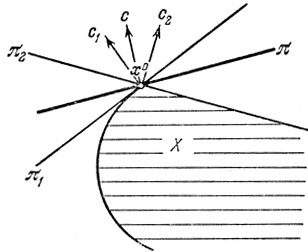
Рис. 2.3
Теорема 2.5.Если множество X0 внутренних точек выпуклого множества X не пусто и не пересекается с выпуклым множеством Y (X0∩Y = ∅). то для множеств X и Y существует разделяющая гиперплоскость π, то есть существует вектор c≠0 такой, что
<с, y>≤<c, x>
для всех y∈Y и x∈X.
Доказательство. Множество
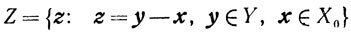
выпукло и z = 0 не является его внутренней точкой.
Тогда из теорем 2.3 и 2.4 следует существование с≠0 такого, что
<c, z> = <c, y - x>≤<c, 0> = 0
для всех y∈Y и x∈X0. Это неравенство остается справедливым и для всех y∈Y и x∈X, поскольку предельный переход не нарушает нестрогих неравенств.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'