2.4. Угловые точки. Теорема о представлении
Определение. Точка x множества X называется угловой (или крайней) точкой, если в X не существует таких точек x' и x", x'≠x", что
x = αx' + (1-α)x"
при некотором α∈(0, 1).
Например, для круга любая точка ограничивающей его окружности является угловой. Угловыми точками являются все вершины выпуклого многогранника.
Определение. Точка x называется выпуклой комбинацией точек x1, x2, ..., xN, если существуют такие числа αi≥0 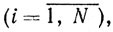
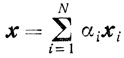
и
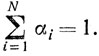
Пример. Любая внутренняя точка круга является выпуклой комбинацией концов хорды, проходящей через точку x.
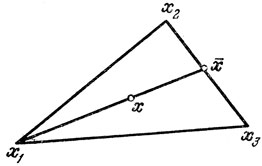
Рис. 2.4
Пример. Легко видеть (рис. 2.4), что любая точка x треугольника является выпуклой комбинацией его вершин x1, x2 и x3:
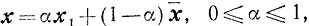
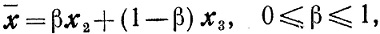
откуда
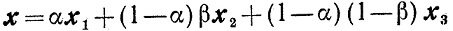
и
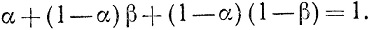
Теорема 2.6 (о представлении). Любая точка x0 выпуклого, замкнутого, ограниченного множества X может быть представлена в виде выпуклой комбинации конечного числа угловых точек этого множества.
Доказательство (по индукции наименьшей размерности n пространства En, содержащего множество X).
Если n = 1, то X является отрезком и утверждение теоремы очевидно.
Предположим, что для n = k - 1 теорема справедлива. Пусть теперь X⊂Ek. Рассмотрим два случая.
1) x0 - граничная точка X. Построим в этой точке гиперплоскость, опорную к X:
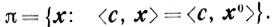
Множество X0 = X∩π, как пересечение выпуклого, замкнутого, ограниченного множества X с выпуклым, замкнутым множеством π, само выпукло, замкнуто и ограничено и, кроме того, существует (k - 1)-мерное подпространство, содержащее X0 (поскольку X0⊂π). По предположению индукции для x0∈X0 найдутся x1, x2, ..., xN - угловые точки множества X0 такие, что
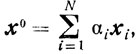
αi≥0 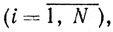
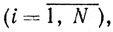
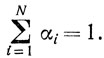
Покажем, что x1, x2, ..., xN являются угловыми точками и для X. Предположим противное, то есть, что для некоторой точки xi найдутся x'∈X, x"∈X, x'≠x" и α∈(0, 1) такие, что
xi = αx' + (1-α)x".(2.7)
Так как xi∈X0⊂π, то
<c, xi> = <c, x0>,(2.8)
и поскольку гиперплоскость π - опорная к X, то
<c, x'> ≤ <c, x0> и <c, x"> ≤ <c, x0>(2.9)
Из того, что 0<α<1б и из (2.7), (2.8), (2.9) следует
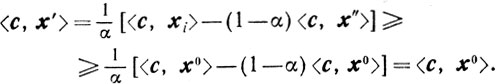 (2.10)
(2.10)Неравенства (2.9) и (2.10) показывают, что x'∈π (так как <c, x'> = <c, x0>); но x'∈X, следовательно, x'∈X0 = X∩π. Аналогично доказывается, что x"∈X0. А тогда предположение (2.7) противоречит тому, что xi - угловая точка X0.
2) Пусть теперь x0 - внутренняя точка множества X. Проведем через x0 прямую l. Пересечение l∩X является отрезком с концами 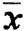 и
и 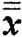 , принадлежащими границе множества X, и поскольку x0 - внутренняя точка для X, то существует α∈(0, 1) такое, что
, принадлежащими границе множества X, и поскольку x0 - внутренняя точка для X, то существует α∈(0, 1) такое, что
x0 = α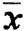 + (1-α)
+ (1-α)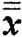 (2.11)
(2.11)
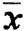 + (1-α)
+ (1-α)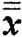 (2.11)
(2.11)
Поскольку для граничных точек 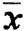 и
и 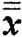 теорема верна, то она верна и для x0. Действительно, для граничных точек имеют место соотношения
теорема верна, то она верна и для x0. Действительно, для граничных точек имеют место соотношения
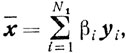
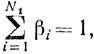
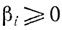
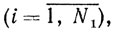
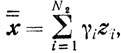
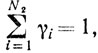
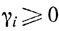
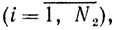
где все yi и zi - угловые точки множества X. Тогда
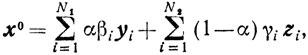
откуда и следует утверждение теоремы.
Задача 2.4. Доказать, что любая точка n-мерного куба
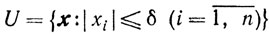
представима в виде выпуклой комбинации его вершин.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'