2.5. Теорема Фаркаша. Конус

В теории математического программирования важную роль играет следующая теорема.

Теорема 2.7 (Фаркаша). Если для произвольной матрицы В существует такой вектор V, что для всех дг, удовлетворяющих неравенству

будет

то всегда найдется вектор u≥0 такой, что

Доказательство. Рассмотрим множество

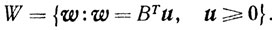
Если v∈W, то теорема доказана. Предположим, что v∉W. Покажем, что в этом случае найдется такой x, что Bx≤0; но <v, x>>0. Это противоречие условиям, и докажет теорему.

Рассмотрим вектор c = v - p, где p - проекция точки v на W. Из теоремы 2.3 следует, что для всех w∈W будет

Но из (2.2) получаем <w - p, v - p>≤0, то есть

Поскольку w = 0∈W, то из (2.12) следует неравенство

и так как w + p ∈W, то из (2.13) получаем

то есть <c, w>≤0. Но

И так как это имеет место для всех u≥0, то

Взяв х = с, из (2.14), (2.15) получаем противоречие условиям теоремы.

Замечание. Доказательство теоремы проведено в молчаливом предположении, что множество W замкнуто (замкнутость гарантирует существование точки p∈W). Множество W и в самом деле замкнуто, доказательству чего будет посвящен следующий раздел.

Прежде чем дать геометрическое истолкование теоремы Фаркаша, введем понятие конуса.

Определение. Множество K⊆E_n называется конусом, если из x∈K следует λx∈K для всех λ≥0.

Очевидно, что множество

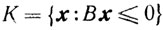
является конусом. Более того, поскольку это множество выпукло и замкнуто, то - выпуклым, замкнутым конусом.

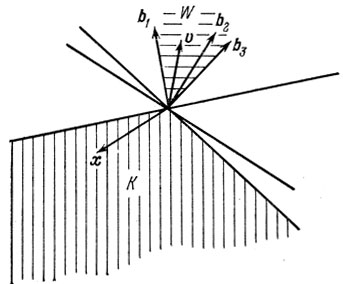
Рис. 2.5

Например, в двумерном случае (рис. 2.5), если

то

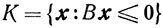
есть совокупность всех векторов x, которые образуют с каждым из векторов b₁, b₂, b₃ неострые углы (на рис. 2.5 конус К заштрихован вертикальными линиями). Множество

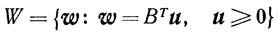
есть также выпуклый конус.

Теперь очевиден геометрический смысл теоремы Фаркаша: чтобы для любого x∈K выполнялось условие <v, x>≤0 (то есть, чтобы угол между v и x был неострым), необходимо, чтобы v принадлежал конусу W.