2.6. Теорема о замкнутости конуса
Доказательство теоремы о замкнутости конуса опирается на два известных утверждения, которые сформулируем как леммы.
Лемма 2.1.Объединение
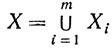
конечного числа замкнутых множеств Xi замкнуто.
Доказательство. Пусть x∉X. Покажем, что существует такая окрестность точки x, которая содержит не более конечного числа точек из X и, следовательно, x не может быть предельной точкой для X.
Так как x∉X, то x не принадлежит ни одному из замкнутых множеств Xi и, следовательно, не является предельной ни для одного из них. Поэтому для каждого i существует окрестность точки x, которая содержит не более конечного числа точек из Xi. Выбрав наименьшую из этих окрестностей, получаем окрестность точки x, содержащую не более чем конечное число точек из X.
Лемма 2.2.Если столбцы (вектор-столбцы) матрицы А линейно-независимы, то линейное преобразование y = Ax отображает замкнутое множество X на замкнутое множество Y.
Доказательство. Поскольку матрица АТА - невырожденная, то из АТy = АТАx следует
x = (АТА)-1АТy.
Замкнутость Y следует из соотношения
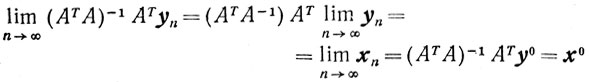
для сходящейся последовательности {yn}→y0 = Ax0.
Теорема 2.8 (о замкнутости конуса). Множество
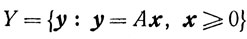
замкнуто.
Доказательство. Пусть Ais = [ai1, ai2, ..., ais] - линейно-независимая подсистема векторов из A = [a1, a2, ..., ak]. Число таких подсистем размерности s≤k конечно (не превосходит Сsk). Рассмотрим всевозможные подсистемы линейно-независимых векторов вида Ais (s = 1, 2, ..., k). Их также конечное число (не превосходящее 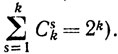 Обозначим
Обозначим
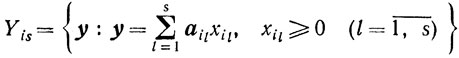
и рассмотрим объединение всех таких множеств:
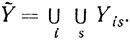
Для доказательства теоремы достаточно показать, что 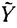 = Y, так как из предыдущих- лемм следует, что
= Y, так как из предыдущих- лемм следует, что 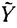 замкнуто.
замкнуто.
Очевидно, что 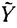 ⊆Y, поскольку если y∈
⊆Y, поскольку если y∈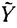 , то найдется Yis такое, что y∈Yis⊆Y. Осталось показать, что Y⊆
, то найдется Yis такое, что y∈Yis⊆Y. Осталось показать, что Y⊆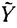 .
.
Рассмотрим произвольный y∈Y. Так как y = 0∈Y и y = 0∈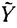 , то достаточно рассмотреть y≠0. Итак,
, то достаточно рассмотреть y≠0. Итак,
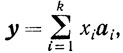
xi≥0, (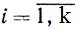 )
)
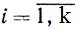 )
)Не ограничивая общности, можно полагать, что первые l чисел x1, x2, ..., хl строго положительны (1≤l≤k), а xl+1 = xl+2 = ... = xk = 0. Тогда
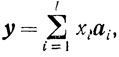
xi>0 (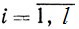 )
)
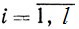 )
)
Если a1, a2, ..., al линейно-независимы, то y∈;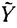 . Пусть a1, a2, ..., al линейно-зависимы, то есть существуют числа αi
. Пусть a1, a2, ..., al линейно-зависимы, то есть существуют числа αi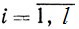 такие, что
такие, что
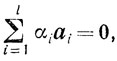
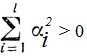
Для определенности будем предполагать, что первые m чисел αi ≠ 0 (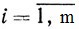 ), а
), а
αm+1 = αm+2 = ... = αl = 0 (m≤l).
Обозначим 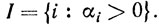 Очевидно, что I≠∅, так как в противном случае вместо
Очевидно, что I≠∅, так как в противном случае вместо 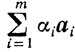 будем рассматривать
будем рассматривать 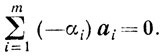 Выберем
Выберем
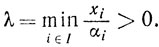
Без ограничения общности можно предположить, что λ = x1/α1. Тогда
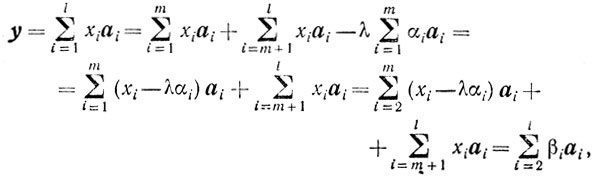
где
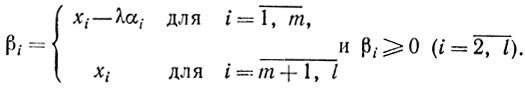
Если система a2, a3, ..., al линейно-независима, то y∈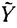 . Если векторы a2, a3, ..., al линейно зависимы, то, повторив процедуру, исключим из этой системы по крайней мере еще один вектор, например a2, таким образом, что
. Если векторы a2, a3, ..., al линейно зависимы, то, повторив процедуру, исключим из этой системы по крайней мере еще один вектор, например a2, таким образом, что
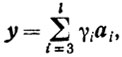
γi≥ 0 (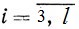 )
)
Повторяя процедуру, через конечное число шагов придем к случаю, когда
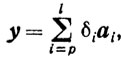
δi≥0 (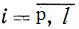 )
)
и ар, ap+1, ... , ai линейно-независимы, откуда следует 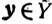 и, значит,
и, значит, 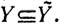
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'