2.7. Выпуклые и вогнутые функции

Определение. Скалярная функция φ (x) называется выпуклой на выпуклом множестве X, если для любых x, y ∈Х и α∈[0, 1] выполняется неравенство

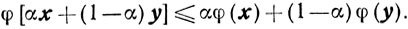(2.16)

Если же

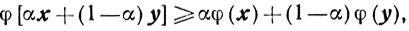(2.17)

то функция φ(x) называется вогнутой.

На рис. 2.6 изображена выпуклая функция. Очевидно, что если φ(x) выпукла, то - φ(x) вогнута.

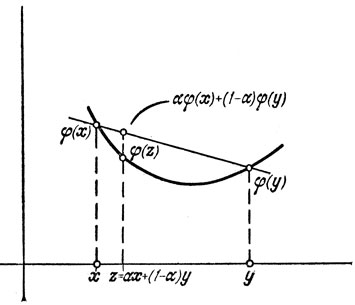
Рис. 2.6

Если для любого α∈ (0, 1) неравенство (2.16) - строгое, то функцию φ(ч) называют строго выпуклой (соответственно для (2.17) - строго вогнутой).

Иногда, в целях упрощения выкладок при различных доказательствах, пользуются следующим определением выпуклости: непрерывная функция φ(х) называется выпуклой на выпуклом множестве X, если для любых x, y ∈Х выполняется условие

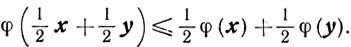
Легко убедиться, что сумма выпуклых (вогнутых) функций является выпуклой (вогнутой) функцией.

Примером выпуклой функции служит квадратичная форма, с положительно определенной матрицей. Поскольку этим свойством квадратичных функций мы будем пользоваться в дальнейших рассмотрениях, сформулируем его как самостоятельную теорему.

Теорема 2.9.Для того чтобы квадратичная функция

была выпуклой, необходимо и достаточно, чтобы симметрическая матрица В была положительно определенной.

Доказательство.

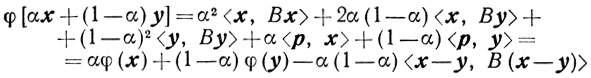
и при α∈(0, 1) будет

в том и только в том случае, если В положительно определена. Отсюда и из определения выпуклости следует утверждение теоремы.

Замечание. Очевидно, что для строгой выпуклости квадратичной функции φ(x) необходима и достаточна строгая положительная определенность матрицы В.

Предпочитаете заниматься трахом в компании обаятельной индивидуалки? Веб сайт https://prostitutkikaliningrada24.com рекомендует попользоваться услугами интимных индивидуалок, которые согласны даже на исследованьи в сексе.