2.8. Дифференцируемость по направлению. Непрерывность

Мы докажем следующие свойства выпуклых функций.

Функция φ(x), выпуклая на выпуклом множестве X, имеет в любой внутренней точке x∈Х производную по любому направлению :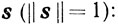

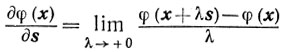
и, более того, выпуклая функция φ(x) непрерывна в каждой внутренней точке x∈Х. Однако эти утверждения не являются верными для граничных точек множества X. В самом деле, на отрезке [0, 1] функция

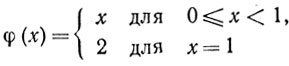
выпукла, но в точке x = 1 терпит разрыв.

Теорема 2.10.Выпуклая функция φ(x), определенная на выпуклом множестве X, имеет в каждой внутренней точке x∈X производную по любому направлению s:

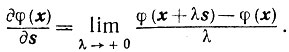
Доказательство. Вначале убедимся, что выпуклая функция ψ (λ) скалярного аргумента λ, определенная на некотором интервале Λ, такова, что величина

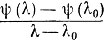
монотонно убывает при λ>λ₀ и λ→λ₀ и ограничена снизу.

Действительно, пусть λ₂<λ₀<λ₁<λ. Так как

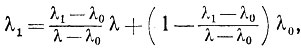
то из выпуклости ψ(λ) получаем

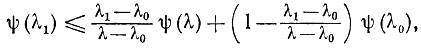
откуда следует

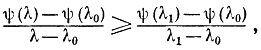
то есть монотонность.

Далее, так как

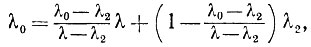
то из выпуклости ψ (λ) получаем

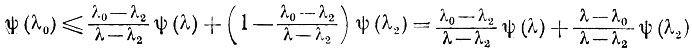
откуда следует

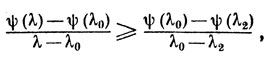
то есть ограниченность.

Таким образом, в любой точке λ₀ интервала Λ существует правосторонняя производная

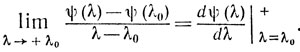
Заметим, что аналогично доказывается и существование левосторонней производной функции ψ(λ).

Наконец, пусть в точке x∈Х задано направление s. Рассмотрим

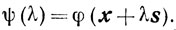
Если х - внутренняя точка множествах, то существует некоторый интервал Λ = (-λ', λ'), в каждой точке которого определена ψ(λ). Очевидно, что ψ(λ) выпукла и, следовательно, существует

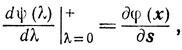
так же, как и

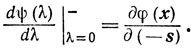
Лемма 2.3.Если ψ(λ) выпукла и

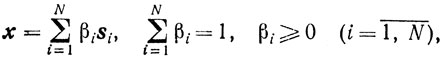
то

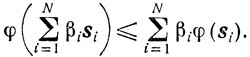
Доказательство проведем по индукции. Для N = 1 лемма очевидна. Предположим, что она верна для N = k. Докажем ее для N = k+1.

При β_k+1 = 1 имеем β₁ = β₂ =...= β_k = 0.

Если 0≤β_k+1≤1, то из выпуклости и индуктивного предположения следует

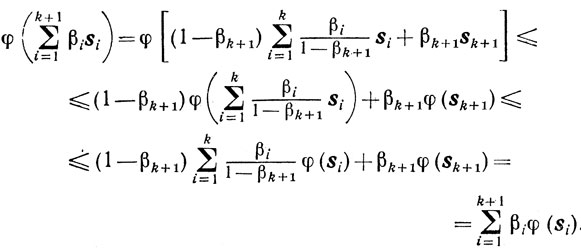
Теорема 2.11.Выпуклая функция φ(х), определенная на выпуклом множестве X, непрерывна в каждой внутренней точке этого множества.

Доказательство. Пусть х⁰ - внутренняя точка множества X. Перенесем начало координат в точку х⁰ и обозначим ψ(y) = φ (y + х⁰). Очевидно, что φ(y) выпукла и 0 является внутренней точкой выпуклого множества

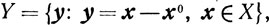
поэтому существует δ₀>0 такое, что для 0<δ≤δ₀ окрестность

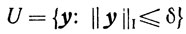
точки 0 принадлежит множеству Y: U⊂Y. Выберем норму || ||, следующим образом:

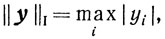
тогда множество U представляет собой n-мерный куб с вершинами s_i:

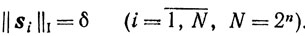
Любая точка y n-мерного куба представима (теорема 2.6, см. также задачу 2.4) в виде выпуклой комбинации вершин

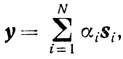
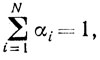
α_i≥0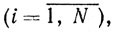

Ввиду леммы 2.3 имеем

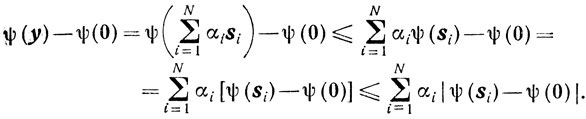
Из дифференцируемости ψ(y) в точке 0 по любому направлению следует, что для каждого s_i найдется такое δ_i>0, что для всех 0<δ≤δ_i будет

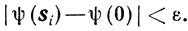
Выбирая

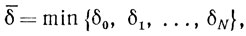
получаем

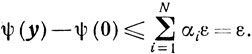
Но так как множеству U вместе с точкой y принадлежит и -y, то аналогично предыдущему получаем

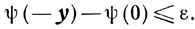
Так как ψ(y) выпукла, то

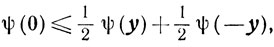
откуда

Таким образом, окончательно приходим к неравенству

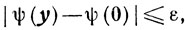
справедливому для всех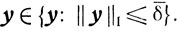

Из непрерывности ψ(y) в нуле вытекает непрерывность φ(x) в точке x⁰.