2.9. Выпуклые дифференцируемые функции
Важное свойство дифференцируемых функций, которым мы будем постоянно пользоваться, устанавливает следующая лемма.
Лемма 2.4. Функция φ(x), дифференцируемая на выпуклом и замкнутом множестве X, выпукла в том и только в том случае, если для любых х∈Х и y∈Х будет
<φ'(x), y-x>≤φ(y)-φ(x).(2.18)
Для вогнутой функции
<φ'(x), y-x>≥φ(y)-φ(x).(2.19)
Доказательство. Запишем для φ(x) условие (2.16) в следующем виде:
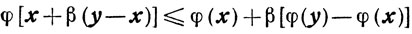
при 0<β≤11,
откуда
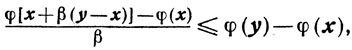
и, переходя к пределу при β→0, получим (2.18). Для этого достаточно рассмотреть функцию одного переменного
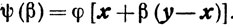
Тогда левая часть последнего неравенства запишется в виде
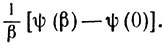
Воспользовавшись правилом дифференцирования сложных функций, получаем
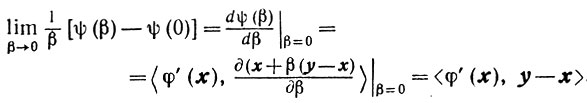
Пусть теперь выполняется условие (2.18). Обозначив
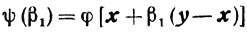
и
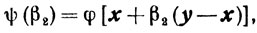
получаем
ψ'(β1)(β2-β1)≤ψ(β2)-ψ(β1)
ψ'(β2)(β1-β2)≤ψ(β1)-ψ(β2)
откуда
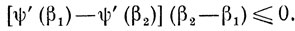
Таким образом, при β2>β1 будет
ψ'(β2)≥ψ'(β1)
Пусть 0<λ<1 и β2>β1; тогда
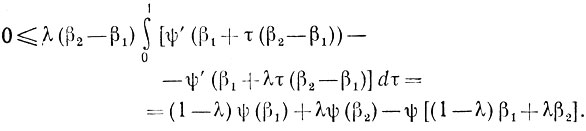
Аналогичный результат получаем и при β2<β1 вследствие чего для любых β1 и β2 будет справедливо неравенство
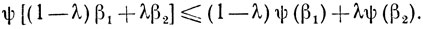
Таким образом, ψ(β) выпукла, а следовательно, выпукла и φ(x):
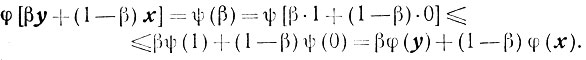
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'