2.12. Некоторые экстремальные свойства функций на выпуклых множествах

В этом разделе будут рассмотрены условия существования экстремальных точек дифференцируемых функций на выпуклых множествах.

Возможные направления. Понятие возможного направления занимает важное место в математическом программировании. Ввиду этого ряд экстремальных свойств будет сформулирован в терминах возможных направлений.

Определение. Направление s≠0 в точке х выпуклого множества X называется возможным, если существует такое число λ₀>0, что для всех λ∈[0, λ₀] будет

Например, если Х = {х: x≥0},то в точке х = 0 любой вектор s≥0, s≠0 задает возможное направление. А в точке

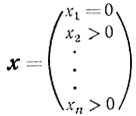
возможным является любое направление

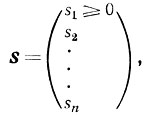
где s₂, s₃, ..., s_n - произвольные числа, s≠0.

Очевидно, если х - внутренняя точка множества X, то любое направление s в этой точке является возможным.

Теорема 2.12.Для того чтобы точка х* выпуклого множества X являлась точкой локального минимума дифференцируемой на X функции φ(х), необходимо, чтобы для всех х ∈ X из достаточно малой окрестности точки х* выполнялось неравенство

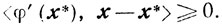
Пусть х* - точка локального минимума. Рассмотрим ε - окрестность точки х*:

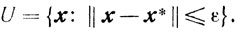
Тогда для всех х ∈ X ∩ U будет

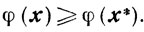
Так как множество X ∩ U выпукло, то любое возможное направление в точке х* может быть представлено в виде s = x-x*, и для 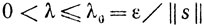будет

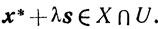
Поэтому

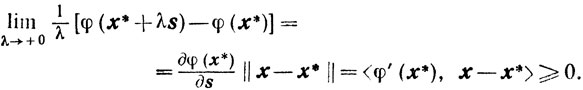
Замечание. В терминах "возможных направлений" эту теорему можно сформулировать следующим образом:

Для того чтобы точка х* выпуклого множества X являлась точкой локального минимума дифференцируемой на X функции φ(x), необходимо, чтобы в этой точке производные по всем возможным направлениям были неотрицательными.

Теорема 2.13.Если выпуклы функция φ(х) и множество X, то любая точка х*∈Х, являющаяся точкой локального минимума, будет оптимальной для задачи минимизации φ(х) на выпуклом множестве X. Множество оптимальных точек выпукло.

Доказательство. Предположим, что х* не является оптимальной точкой, то есть найдется х'∈Х такая, что

Рассмотрим точки вида

Так как множество X выпукло, то х ∈ X. Далее, из выпуклости φ (х) и из предположения об х' следует

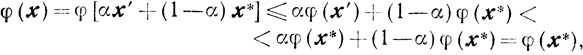
то есть

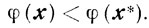
Но это противоречит условию, что х* - точка локального минимума, поскольку при малых а точка х находится в достаточно малой окрестности точки х*. Наконец, убедимся, что множество

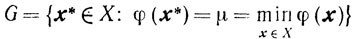
выпукло. Действительно, пусть х'∈G и x"∈G. Поскольку G⊆X, а X выпукло, то для 0≤λ≤1 будет

а ввиду выпуклости φ(x) имеем

С другой стороны, поскольку μ - минимальное значение φ(x) на X, то

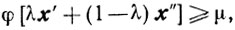
откуда

то есть G выпукло.

Теорема 2.14.Для того чтобы точка х* выпуклого множества X являлась точкой минимума выпуклой и дифференцируемой на X функции φ(х), то есть оптимальной точкой, необходимо и достаточно, чтобы для любого x ∈ X выполнялось неравенство

Необходимость. Следует из двух предыдущих теорем.

Достаточность. Пусть для любой точки х∈Х будет

Из выпуклости φ(x) следует

то есть x* оптимальна.

Теорема 2.15.Если φ(x) строго выпукла на выпуклом множестве X и точка х* ∈ X оптимальна, то есть

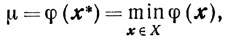
то для всех х ∈ X и х ≠ х* будет

и значит, точка х* единственна.

Доказательство. Предположим, что найдется точка x'∈Х и х*≠х' такая, что

Тогда для любого α∈(0, 1] точка x = αx' + (1-α)x* принадлежит множеству X и в силу строгой выпуклости функции φ (х) будет

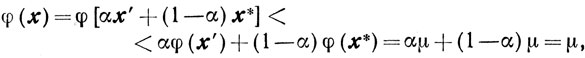
что противоречит оптимальности точки х*.

Наконец, рассмотрим еще один критерий оптимальности. Пусть

где число v>0 - любое. Обозначим через p = p(v) проекцию точки v на множество X.

Теорема 2.16.Для того чтобы точка х* выпуклого множества X являлась точкой минимума выпуклой и дифференцируемой на X функции φ(х), необходимо и достаточно, чтобы

где v* = x*-vφ'(x*).

Доказательство.

Достаточность. Пусть x* = p (v*). Так как р (v*) есть проекция точки v* на X, то из (2.2) получаем для всех х∈Х неравенство

И так как v* = x* - vφ' (х*) и v>0 то, следовательно,

то есть, по теореме 2.14, х*-точка минимума.

Необходимость. Пусть х* - точка минимума. Тогда для любого х∈Х будет

или

Но -v<φ'(x*). х-x*>≥0, следовательно,

то есть х* в силу теоремы 2.2 есть проекция точки v* на X:

Замечание.Легко убедиться, что если освободить φ(х) от требований выпуклости, то будет справедливо следующее утверждение:

Для того чтобы точка х* выпуклого множества X являлась точкой локального минимума дифференцируемой на X функции φ(х), необходимо, чтобы