2.13. Сильная выпуклость функций

Мы видели, что если для выпуклой функции φ(х) существует точка локального минимума на выпуклом и замкнутом множестве X, то она является оптимальной, а для строго выпуклой функции эта точка вдобавок и единственна. Рассмотрим теперь один класс функций, Для которых на любом непустом замкнутом множестве всегда существует точка минимума, и если вдобавок Это множество выпукло, то эта точка единственна.

Определение. Функцию φ(x), определенную на выпуклом множестве X, будем называть сильно выпуклой, если существует константа р>0 такая, что для любых x, y ∈ X и α∈[0, 1] будет выполняться неравенство

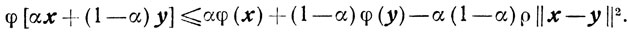(2.20)

Величину р в дальнейшем будем называть параметром сильной выпуклости.

Приведем пример сильно выпуклой функции. Рассмотрим квадратичную функцию

где В - строго положительно определенная матрица. Сильная выпуклость следует из соотношения

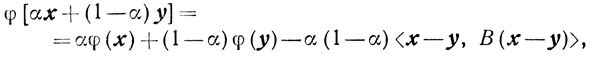
поскольку

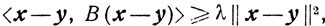
где λ - наименьшее собственное число матрицы В.

Укажем на некоторые свойства сильно выпуклых функций.

Свойство 1. Если φ (х) ∈ С¹ (X) сильно выпукла на выпуклом множестве X, то для всех x, y ∈ X справедливо неравенство

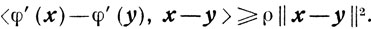(2.21)

Действительно, так как функция φ(х) выпукла, то

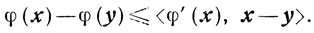
Отсюда и из определения сильной выпуклости получаем

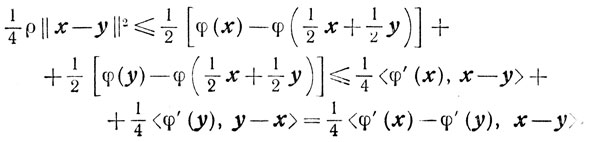
Свойство 2. Если функция φ(х) сильно выпукла на выпуклом замкнутом множестве X, то

1) Для любой точки х⁰ множество

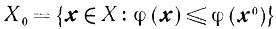
ограничено;

2) существует единственная точка х* такая, что

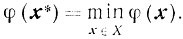
Доказательство. Доказательство проведем в предположении, что φ (х) ∈ С¹ (X). Свойство справедливо и без этого предположения^*, однако доказательство будет более громоздким.

Так как

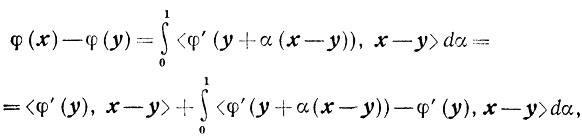
то, пользуясь неравенством (2.21), получаем

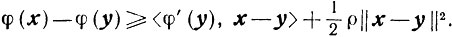(2.22)

Отсюда следует

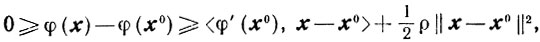
поэтому

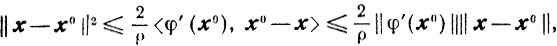
откуда получаем для всех х∈Х₀

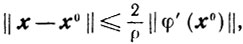(2.23)

то есть ограниченность множества Х₀.

^* (См. [2].)

Существование х* очевидно, так как из непрерывности φ(х) на ограниченном множестве Х₀ и из определения Х₀ следует

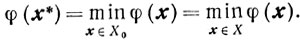
Единственность же точки х* следует из того, что сильно выпуклая функция является в то же время строго выпуклой, -и из теоремы 2.15.

Свойство 3. Если φ(x) сильно выпукла на выпуклом и замкнутом множестве X, то для всех х∈Х справедливо неравенство

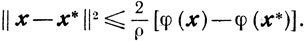(2.24)

Если при этом φ(х)∈С¹(Х), то

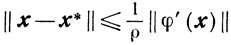(2.25)

и

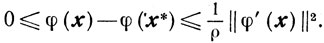(2.26)

Доказательство. Из (2.20) следует

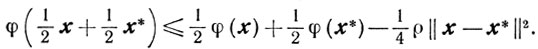
И так как

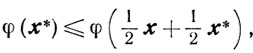
то получаем (2.24). В точке х* минимума φ(x) на X выполняется для всех х ∈ X неравенство (см. теорему 2.14)

поэтому из (2.21) получаем

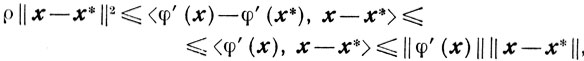
то есть (2.25).

Наконец, из (2.18) и (2.25) имеем

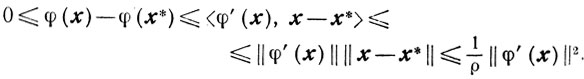
Свойство 4. Если сильно выпуклая функция φ(x) принадлежит классу С^1,1(Х) на выпуклом замкнутом множестве X, то есть существует такая константа L>0, что для любых x, y ∈ X

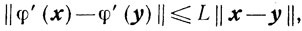
то для любых x, y ∈ Х таких, что φ (х)≤φ(y), будет выполняться неравенство

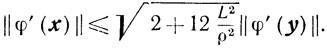(2.27)

Доказательство. Если φ'(y) = 0, то и φ'(x) = 0 и, следовательно, (2.27) выполняется. Пусть теперь φ'(y) ≠ 0. Из соотношения

следует справедливость неравенства

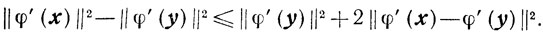
Предположим теперь, что свойство 4 неверно, то есть найдутся такие x, y ∈ Х, что

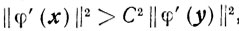
где

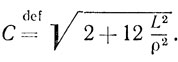
Тогда

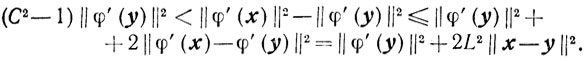
Но так как φ(x)≤φ(y), то из (2.24), (2.25) и (2.26) получаем

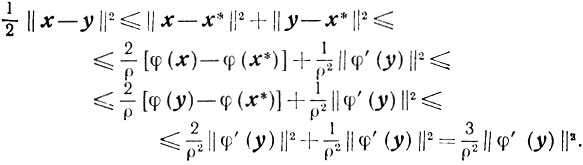
Поэтому

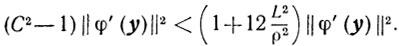
И так как 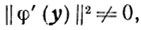то приходим к неравенству

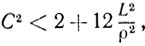
противоречащему определению величины С.